练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2cos25°-cos85°
    sin25°+
    		3
    cos25°
    =
     
    ．
    考点：两角和与差的正弦函数
    专题：三角函数的求值
    分析：由两角和与差的正弦函数公式展开后根据诱导公式化简即可求值．
    解答： 解：
    2cos25°-cos85°
    sin25°+
    		3
    cos25°
    =
    2sin65°-sin5°
    2sin(25°+60°)
    =
    2sin60°cos5°+2cos60°sin5°-sin5°
    2cos5°
    =
    		3
    cos5°
    2cos5°
    =
    		3
    2
    ．
    故答案为：
    		3
    2
    ．
    点评：本题主要考查了两角和与差的正弦函数公式，诱导公式化简求值，属于基本知识的考查．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知命题p：x2-2x-3＞0，命题q：
    1
    3-x
    ＞    1，若￢q且p为真．则x的取值范围
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图是某一个几何体的三视图，则该几何体的体积为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知（
    		21
    +5）sinθ-7cosθ=2-
    		21
    ，求sinθ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    m
    =（cos
    x
    2
    ，-1），
    n
    =（
    		3
    sin
    x
    2
    ，cos2
    x
    2
    ），设函数f（x）=
    m
    •
    n
    +1．
    （Ⅰ）求f（x）的单调区间；
    （2）若x∈[0，
    π
    2
    ]，f（x）=
    11
    10
    ，求cosx值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）为奇函数，且在（-∞，0）内是增函数，又f（-2）=0，则f（x）＜0的解集为（　　）
    A、（-2，0）∪（0，2）
    B、（-∞，-2）∪（0，2）
    C、（-∞，-2）∪（2，+∞）
    D、（-2，0）∪（2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

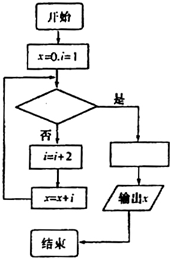    如图是某同学求50个奇数3，5，7，…，101的平均数而设计的程序框图的部分内容，则在该程序框图中的空白判断框和处理框中应填入的内容依次是（　　）
    A、i＞100，x=
    x
    50
    B、i≥100，x=
    x
    100
    C、i＜100，x=
    x
    50
    D、i≤100，x=
    x
    100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

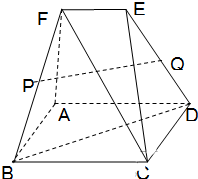    如图，多面体ABCDEF中，四边形ABCD是边长为2a的正方形，平面ADEF垂直于平面ABCD，且FA⊥AD，EF∥AD，EF=AF=a．
    （1）求证：BD⊥CF；
    （2）若P、Q分别为棱BF和DE的中点，求证：PQ∥平面ABCD；
    （3）求多面体ABCDEF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}满足a1=1，an+an+1=an2+bn+1（a，b为常数，n∈N*）
    （1）如果{an}为等差数列，求a，b的值；
    （2）如果{an}为单调递增数列，求a+b的取值范围．

    查看答案和解析>>

    同步练习册答案