
 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知$\frac{sinB}{sinA+sinC}$=$\frac{a+b-c}{a+b}$.
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知$\frac{sinB}{sinA+sinC}$=$\frac{a+b-c}{a+b}$.分析 (1)由正弦定理化简已知整理可得b2+c2-a2=bc,由余弦定理可得cosA=$\frac{1}{2}$,结合范围A∈(0,π),即可求A.
(2)求出∠A1AC,由三角形性质知,边所对应角最小时,边长最小,当∠A1AC=θ-30°=0时,即可求A1C的最小值.
解答 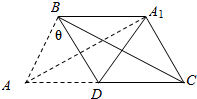 解:(1)在△ABC中,∵$\frac{sinB}{sinA+sinC}$=$\frac{a+b+c}{a+b}$=$\frac{b}{a+c}$,∴整理可得:b2+c2-a2=bc,
解:(1)在△ABC中,∵$\frac{sinB}{sinA+sinC}$=$\frac{a+b+c}{a+b}$=$\frac{b}{a+c}$,∴整理可得:b2+c2-a2=bc,
∴由余弦定理可得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$,
∵A∈(0,π),
∴A=$\frac{π}{3}$.
(2)以BD为折痕,将△ABD折到与△ADC到同一个平面内,
设∠ABD=θ.则AB=BA1,∠ABD=∠A1BD=θ,
∴∠A1AC=60°-$\frac{180°-2θ}{2}$=θ-30°,
由三角形性质知,边所对应角最小时,边长最小,故当∠A1AC=θ-30°=0时,A1C最小,
即θ=30°,
可知BD⊥AC,BD=6,
则AA1=4$\sqrt{3}$,得出A1C=AC-AA1=8$\sqrt{3}-4\sqrt{3}$=4$\sqrt{3}$,
∴A1C的最小值为4$\sqrt{3}$.
点评 本题考查利用数学知识解决实际问题,考查正弦定理,余弦定理的应用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(2,+∞) | C. | (-∞,-2)∪(0,2) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com