
 中,
中, 是正方形,E是
是正方形,E是 的中点,
的中点,
 ,求 PC与面AC所成的角
,求 PC与面AC所成的角 平面
平面
 (2)先证明EO∥PC (3)先证明BC^平面PAB
(2)先证明EO∥PC (3)先证明BC^平面PAB ,由于
,由于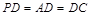 ,则
,则 ;第二问,关键是证明EO∥PC,由于EO是三角形PAC的中位线,则EO∥PC,结合直线与平面平行的判定定理,只要在说明PC
;第二问,关键是证明EO∥PC,由于EO是三角形PAC的中位线,则EO∥PC,结合直线与平面平行的判定定理,只要在说明PC 平面EBD,EO
平面EBD,EO 平面EBD,就可以下结论PC∥平面EBD;第(3)问,先证明PD^BC和BC^CD,则BC^平面PAB,又因为BC
平面EBD,就可以下结论PC∥平面EBD;第(3)问,先证明PD^BC和BC^CD,则BC^平面PAB,又因为BC 平面PBC,所以就有平面PBC^平面PCD。
平面PBC,所以就有平面PBC^平面PCD。
 平面
平面 ,
, 是直线
是直线 在平面
在平面 上的射影,
上的射影, 是直线
是直线 和平面
和平面 所成的角。又
所成的角。又 ,四边形
,四边形 是正方形,
是正方形,
 ,
, ;
;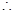 直线
直线 和平面
和平面 所成的角为
所成的角为
 平面EBD,EO
平面EBD,EO 平面EBD ∴PC∥平面EBD
平面EBD ∴PC∥平面EBD 平面ABCD,∴PD^BC,
平面ABCD,∴PD^BC, 平面PCD
平面PCD 平面PBC,∴平面PBC^平面PCD
平面PBC,∴平面PBC^平面PCD

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:不详 题型:解答题
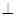 BQ并说明理由.
BQ并说明理由.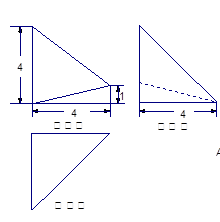
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 体积的水,密封后可以任意摆放,那么容器内水面形状可能是:①三角形;②梯形;③长方形;④五边形.
体积的水,密封后可以任意摆放,那么容器内水面形状可能是:①三角形;②梯形;③长方形;④五边形.| A.①②③ | B.①③④ | C.②③④ | D.①②③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
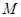 是
是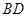 的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧(左)视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.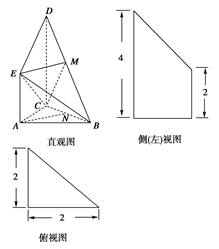
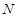 是
是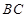 的中点,求证:
的中点,求证: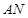 ∥平面
∥平面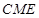 ;
;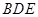 ⊥平面
⊥平面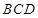 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.0 | B.8 | C.奥 | D.运 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com