
【题目】如图,已知在三棱台![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
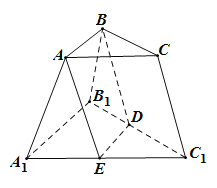
(1)求证:![]() ;
;
(2)过![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且分割三棱台
,且分割三棱台![]() 所得两部分几何体的体积比为
所得两部分几何体的体积比为![]() ,几何体
,几何体![]() 为棱柱,求
为棱柱,求![]() 的长.
的长.
提示:台体的体积公式![]() (
(![]() ,
,![]() 分别为棱台的上、下底面面积,
分别为棱台的上、下底面面积,![]() 为棱台的高).
为棱台的高).
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2017年最严环保使得各地空气质量指数(![]() )得到了很大的改善,2018年环保部将会更加突出大气、水、土壤三大领域污染治理,继续实施和深化环保领域改革,强化环境执法督察.某市设有12个空气监测站点,其中在轻度污染区、中度污染区、重度污染区分别设有3、6、3个监测点.以这12个站点测得的
)得到了很大的改善,2018年环保部将会更加突出大气、水、土壤三大领域污染治理,继续实施和深化环保领域改革,强化环境执法督察.某市设有12个空气监测站点,其中在轻度污染区、中度污染区、重度污染区分别设有3、6、3个监测点.以这12个站点测得的![]() 的平均值作为该市的空气质量指标.
的平均值作为该市的空气质量指标.
(Ⅰ)若某日的![]() 为120,已知测得轻度污染区的
为120,已知测得轻度污染区的![]() 的平均值为80,中度污染区
的平均值为80,中度污染区![]() 的平均值为116,求重度污染区
的平均值为116,求重度污染区![]() 的平均值;
的平均值;
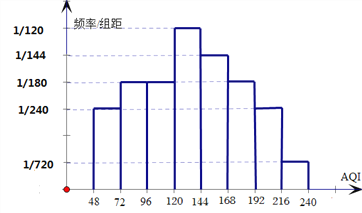
(Ⅱ)如图是2017年11月的30天的![]() 值的频率分布直方图,其中分段区间分别为
值的频率分布直方图,其中分段区间分别为![]() ,11月份仅有1天的
,11月份仅有1天的![]() 在
在![]() 之间.
之间.
①求11月的![]() 低于150的概率;
低于150的概率;
②双创活动中,验收小组要从中度污染区和重度污染区中按比例抽取六个监测点,然后从这六个监测点中随机抽取3个对监测数据进行核实,求至少抽到一个重度污染区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列![]() 中,
中,![]() ,点
,点![]() 在函数
在函数![]() 的图象上,其中
的图象上,其中![]() 为正整数.
为正整数.
(1)证明数列![]() 是“平方递推数列”,且数列
是“平方递推数列”,且数列![]() 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前![]() 项积为
项积为![]() ,即
,即![]() ,求
,求![]() ;
;
(3)在(2)的条件下,记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ,并求使
,并求使![]() 的
的![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,定义
,定义![]() 为
为![]() 的“优值”.现已知某数列的“优值”为
的“优值”.现已知某数列的“优值”为 ![]() ,记数列
,记数列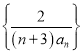 的前
的前![]() 项和为
项和为![]() ,若对一切的
,若对一切的![]() ,都有
,都有![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为___________.
的取值范围为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
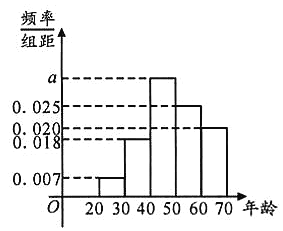
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与抛物线的另一交点分别为两点
与抛物线的另一交点分别为两点![]() 、
、![]() ,连接
,连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 、
、![]() .
.
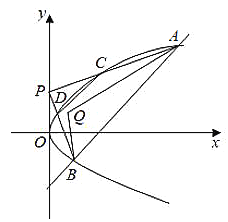
(1)证明:![]() ;
;
(2)若![]() 的面积
的面积![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ).对于不相等的实数
).对于不相等的实数![]() ,
,![]() ,设
,设![]() ,
,![]() 下列说法正确的是( )
下列说法正确的是( )
A.对于任意不相等的实数![]() ,
,![]() ,都有
,都有![]() ;
;
B.对于任意的![]() 及任意不相等的实数
及任意不相等的实数![]() ,
,![]() ,都有
,都有![]() ;
;
C.对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() ,
,![]() ,使得
,使得![]() ;
;
D.对于任意的![]() ,存在不相等的实数
,存在不相等的实数![]() ,
,![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
年龄(单位:岁) |
|
|
|
|
|
保费(单位:元) |
|
|
|
|
|
(1)求频率分布直方图中实数![]() 的值,并求出该样本年龄的中位数;
的值,并求出该样本年龄的中位数;
(2)现分别在年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中各选出
中各选出![]() 人共
人共![]() 人进行回访.若从这
人进行回访.若从这![]() 人中随机选出
人中随机选出![]() 人,求这
人,求这![]() 人所交保费之和大于
人所交保费之和大于![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com