
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 轴的非负半轴为极轴,原点
轴的非负半轴为极轴,原点![]() 为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线
为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线![]() 和
和![]()
![]() 分别与曲线
分别与曲线![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() ,
,![]() 两点异于坐标原点).
两点异于坐标原点).
(1)求曲线![]() 的普通方程与
的普通方程与![]() 、
、![]() 两点的极坐标;
两点的极坐标;
(2)求直线![]() 的极坐标方程及
的极坐标方程及![]() 的面积.
的面积.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排;
(2)排成前后两排,前排4人,后排3人;
(3)全体排成一排,甲不站排头也不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
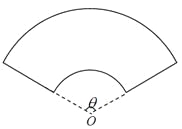
【题目】某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求证: ![]() .
.
(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)求证:对![]() 直线
直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)是否存在实数![]() ,使得圆
,使得圆![]() 上有四个点到直线
上有四个点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围,若不存在,说明理由.
的范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 轴的非负半轴为极轴,原点
轴的非负半轴为极轴,原点![]() 为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线
为极点建立极坐标系,两种坐标系中取相同的长度单位,若直线![]() 和
和![]()
![]() 分别与曲线
分别与曲线![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() ,
,![]() 两点异于坐标原点).
两点异于坐标原点).
(1)求曲线![]() 的普通方程与
的普通方程与![]() 、
、![]() 两点的极坐标;
两点的极坐标;
(2)求直线![]() 的极坐标方程及
的极坐标方程及![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周脾算经》有记载:一年有二十四个节气,每个节气晷(gui)长损益相同,晷是按照日影测定时刻的仪器,晷长即所测定的影子的长度,二十四节气及晷长变化如图所示,相邻两个节气晷长变化量相同,周而复始,若冬至晷长最长是一丈三尺五寸,夏至晷长最短是一尺五寸,(一丈等于10尺,一尺等于10寸),则秋分节气的晷长是( )
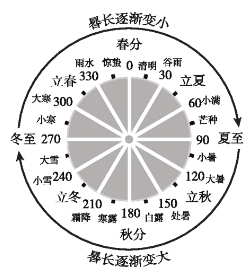
A.七尺五寸B.二尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com