
【题目】已知函数![]() ,其中
,其中![]()
(1)若函数![]() 在区间
在区间![]() 上不单调,求
上不单调,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 在区间
在区间![]() 上有极大值
上有极大值![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由函数![]() ,其中x>0,a∈R.可得
,其中x>0,a∈R.可得![]() .由题意可得:
.由题意可得:![]() 在区间(1,+∞)上有解,分离参数可得:
在区间(1,+∞)上有解,分离参数可得:![]()
![]() 上有解.设
上有解.设![]() ,利用到时讨论其的单调性即可得出.
,利用到时讨论其的单调性即可得出.
(2)当a≥0时,函数f(x)在[1,+∞)上单调递增,此时无极值.
当![]() 时,函数f(x)在[1,+∞)上单调递减,此时无极值.
时,函数f(x)在[1,+∞)上单调递减,此时无极值.
当![]() 时,
时,![]() ,得
,得![]() ..(其中
..(其中![]() )
)
.所以函数f(x)在[1,α)上单调递减,在(α,β)上单调递增,在(β,+∞)上单调递减,由极大值![]() ,又aβ2+β-1=0,消去a利用导数研究函数的单调性进而得出.
,又aβ2+β-1=0,消去a利用导数研究函数的单调性进而得出.
(1)因为![]() ,
,
所以![]() 上有解,
上有解,
所以![]()
![]() 上有解.
上有解.
设![]()
所以函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
所以![]()
![]()
经验证,当![]() 时,函数
时,函数![]() 上单调,
上单调,
所以![]() .
.
(2)当![]() 所以
所以![]() .
.
当![]() 时,
时,![]() 所以
所以![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() .
.
(其中![]() )
)
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
由极大值![]() .
.
又![]()
![]()
设函数![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
而![]() 所以
所以![]()
故当![]() 时,
时,![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,P是椭圆的上顶点,过点P作斜率为
,P是椭圆的上顶点,过点P作斜率为![]() 的直线l交椭圆于另一点A,设点A关于原点的对称点为B
的直线l交椭圆于另一点A,设点A关于原点的对称点为B
(1)求![]() 面积的最大值;
面积的最大值;
(2)设线段PB的中垂线与y轴交于点N,若点N在椭圆内部,求斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
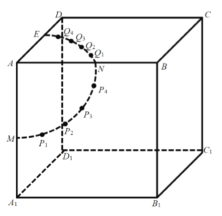
【题目】如图,棱长为2的正方体![]() 中,点
中,点![]() 分别为棱
分别为棱![]() 的中点,以
的中点,以![]() 为圆心,1为半径,分别在面
为圆心,1为半径,分别在面![]() 和面
和面![]() 内作弧
内作弧![]() 和
和![]() ,并将两弧各五等分,分点依次为
,并将两弧各五等分,分点依次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只蚂蚁欲从点
.一只蚂蚁欲从点![]() 出发,沿正方体的表面爬行至
出发,沿正方体的表面爬行至![]() ,则其爬行的最短距离为________.参考数据:
,则其爬行的最短距离为________.参考数据:![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学教师在甲、乙两个平行班采用“传统教学”和“高效课堂”两种不同的教学模式进行教学实验.为了解教改实效,期中考试后,分别从两个班中各随机抽取![]() 名学生的数学成绩进行统计,得到如下的茎叶图:
名学生的数学成绩进行统计,得到如下的茎叶图:
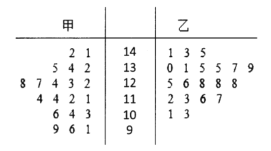
(1)求甲、乙两班抽取的分数的中位数,并估计甲、乙两班数学的平均水平和分散程度(不要求计算出具体值,给出结论即可);
(2)若规定分数在![]() 的为良好,现已从甲、乙两班成绩为良好的同学中,用分层抽样法抽出
的为良好,现已从甲、乙两班成绩为良好的同学中,用分层抽样法抽出![]() 位同学参加座谈会,要再从这
位同学参加座谈会,要再从这![]() 位同学中任意选出
位同学中任意选出![]() 人发言,求这
人发言,求这![]() 人来自不同班的概率.
人来自不同班的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,已知的有中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重的疾病,新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株,某小区为进一步做好新型冠状病毒肺炎疫情知识的教育,在小区内开展“新型冠状病毒防疫安全公益课”在线学习,在此之后组织了“新型冠状病毒防疫安全知识竞赛”在线活动.已知进入决赛的分别是甲、乙、丙、丁四位业主,决赛后四位业主相应的名次为第1,2,3,4名,该小区为了提高业主们的参与度和重视度,邀请小区内的所有业主在比赛结束前对四位业主的名次进行预测,若预测完全正确将会获得礼品,现用![]() 表示某业主对甲、乙、丙、丁四位业主的名次做出一种等可能的预测排列,记
表示某业主对甲、乙、丙、丁四位业主的名次做出一种等可能的预测排列,记![]() .
.
(1)求出![]() 的所有可能情形;
的所有可能情形;
(2)若![]() 会有小礼品赠送,求该业主获得小礼品的概率,
会有小礼品赠送,求该业主获得小礼品的概率,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com