
| A. | 二进制数11010(2)化为八进制数为42(8) | |
| B. | 若扇形圆心角为2弧度,且扇形弧所对的弦长为2,则这个扇形的面积为$\frac{1}{si{n}^{2}1}$ | |
| C. | 用秦九韶算法计算多项式f(x)=3x6+5x4+6x3-4x-5当x=3时的值时,v1=3v0+5=32 | |
| D. | 正切函数在定义域内为单调增函数 |
分析 A.先根据二进制和十进制的关系求出十进制的数,然后在求出八进制的数进行判断,
B.根据圆心角和扇形的面积公式进行求解,
C.根据秦九韶算法进行计算即可.
D.根据正切函数的单调性进行判断.
解答 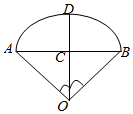 解:A.二进制数11010(2)=1×24+1×23+0×22+1×21+0×20=26.
解:A.二进制数11010(2)=1×24+1×23+0×22+1×21+0×20=26.
∵26÷8=3…2
3÷8=0…3
∴26(10)=32(8)故A错误,
B.如图:设∠AOB=2,AB=2,过点0作OC⊥AB,C为垂足,
并延长OC交$\widehat{AB}$于D,则∠AOD=∠BOD=1,AC=$\frac{1}{2}$AB=1.
Rt△AOC中,r=AO=$\frac{AC}{sin∠AOC}$=$\frac{1}{sin1}$,
从而弧长为l=α•r=2×$\frac{1}{sin1}$=$\frac{2}{sin1}$,
则这个扇形的面积为S=$\frac{1}{2}lr$=$\frac{1}{si{n}^{2}1}$,故B正确,
C.由秦九韶算法可得f(x)=(((((3x+5)x+6)x+0)x-4)x-5),
当x=3时,可得v0=3,v1=2-12=-10,v2=-10×2+60=40,v3=40×2-160=-80.
v0=a6=3,v1=v0x+a5=3×3+5=14,故C错误,
D.正切函数在每一个区间内(kπ-$\frac{π}{2}$,kπ+-$\frac{π}{2}$)为单调增函数,但在定义域内不是单调函数,故D错误,
故选:B
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,有一定的难度.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
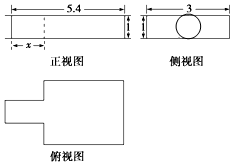 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为( )| A. | 1.2 | B. | 1.6 | C. | 1.8 | D. | 2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=$\sqrt{3}$,SE⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
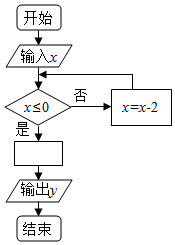 如图是一个算法的程序框图,当输入的x值为1时,输出y的结果恰好是$\frac{1}{2}$,则空白框处所填关系式可以是( )
如图是一个算法的程序框图,当输入的x值为1时,输出y的结果恰好是$\frac{1}{2}$,则空白框处所填关系式可以是( )| A. | y=x2 | B. | y=$\frac{1}{x}$ | C. | y=2x | D. | y=2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的五面体ABCDFE中,四边形ABCD是矩形,AB∥EF,AD⊥平面ABEF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,P、Q分别为AE、BD的中点.
如图所示的五面体ABCDFE中,四边形ABCD是矩形,AB∥EF,AD⊥平面ABEF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,P、Q分别为AE、BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com