
 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.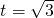 ;
; 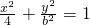 ,将A2(1,t)代入,
,将A2(1,t)代入,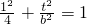 ,得
,得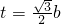 ;
; 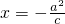 ,
,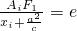 ,则
,则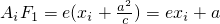 ,(其中
,(其中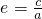 为椭圆的离心率)
为椭圆的离心率)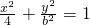 ,因为AiF1+AiF2=4,由椭圆定义知点A2(1,t)在椭圆上,代入椭圆方程即可用b表示t;
,因为AiF1+AiF2=4,由椭圆定义知点A2(1,t)在椭圆上,代入椭圆方程即可用b表示t;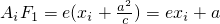 ,新教材实验区的学生可不解第三小题,请学习时注意
,新教材实验区的学生可不解第三小题,请学习时注意 

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.查看答案和解析>>
科目:高中数学 来源:2010年湖北省高考数学模拟试卷(文理合卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com