
【题目】在公差不为零的等差数列{an}中,a2=1,a2、a4、a8成等比数列.
(1)求数列{an}的通项公式an;
(2)设数列{an}的前n项和为Sn , 记bn= ![]() .Tn=b1+b2+…+bn , 求Tn .
.Tn=b1+b2+…+bn , 求Tn .
【答案】
(1)解:公差d不为零的等差数列{an}中,满足a2=1,a2、a4、a8成等比数列.
∴a1+d=1, ![]() =a2a8即(1+2d)2=1×(1+6d),
=a2a8即(1+2d)2=1×(1+6d),
解得 ![]() .
.
∴an= ![]() =
= ![]()
(2)解:由(1)可得:Sn= ![]() =
= ![]() .
.
∴bn= ![]() =
= ![]() =4
=4 ![]() .
.
∴Tn=b1+b2+…+bn= ![]() +…+
+…+ ![]() ]=4
]=4 ![]() =
= ![]()
【解析】(1)公差d不为零的等差数列{an}中,满足a2=1,a2、a4、a8成等比数列.可得a1+d=1, ![]() =a2a8即(1+2d)2=1×(1+6d),解出即可得出.(2)由(1)可得:Sn=
=a2a8即(1+2d)2=1×(1+6d),解出即可得出.(2)由(1)可得:Sn= ![]() .可得bn=
.可得bn= ![]() =
= ![]() =4
=4 ![]() .利用“裂项求和”即可得出.
.利用“裂项求和”即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系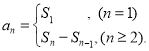 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
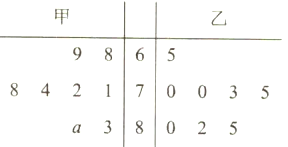
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①已知-1<a<b<0,则0.3a>a2>ab;
②若正实数a、b满足a+b=1,则ab有最大值![]() ;
;
③若正实数a、b满足a+b=1,则![]() 有最大值
有最大值![]() ;
;
④x,y∈(0,+∞),x3+y3>x2y+xy2.
其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的焦点坐标是F1(﹣1,0)、F2(1,0),过点F2垂直于长轴的直线l交椭圆C于B、D两点,且|BD|=3.
(1)求椭圆C的方程;
(2)过定点P(0,2)且斜率为k的直线l与椭圆C相交于不同两点M,N,试判断:在x轴上是否存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形?若存在,求出实数m的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+log2x+b在区间( ![]() ,4)上有零点,则实数b的取值范围是( )
,4)上有零点,则实数b的取值范围是( )
A.(﹣10,0)
B.(﹣8,1)
C.(0,10)
D.(1,12)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个班级共有105名学生,某次数学考试按照“大于等于85分为优秀,85分以下为非优秀”的原则统计成绩后,得到如下![]() 列联表。
列联表。
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知从甲、乙两个班级中随机抽取1名学生,其成绩为优秀的概率为![]() .
.
(1)请完成上面的![]() 列联表;
列联表;
(2)能否有把握认为成绩与班级有关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com