
【题目】如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2 ![]() ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点. 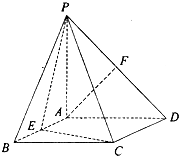
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD;
(3)求四面体PEFC的体积.
【答案】
(1)证明:设G为PC的中点,连接FG,EG,
∵F为PD的中点,E为AB的中点,
∴FG ![]()
![]() CD,AE
CD,AE ![]()
![]() CD
CD
∴FG ![]() AE,∴AF∥GE
AE,∴AF∥GE
∵GE平面PEC,
∴AF∥平面PCE
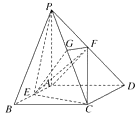
(2)证明:∵PA=AD=2,∴AF⊥PD
又∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD,∵AD⊥CD,PA∩AD=A,
∴CD⊥平面PAD,
∵AF平面PAD,∴AF⊥CD.
∵PD∩CD=D,∴AF⊥平面PCD,
∴GE⊥平面PCD,
∵GE平面PEC,
∴平面PCE⊥平面PCD
(3)由(2)知,GE⊥平面PCD,
所以EG为四面体PEFC的高,
又GF∥CD,所以GF⊥PD,
EG=AF= ![]() ,GF=
,GF= ![]() CD=
CD= ![]() ,
,
S△PCF= ![]() PDGF=2.
PDGF=2.
得四面体PEFC的体积V= ![]() S△PCFEG=
S△PCFEG= ![]()
【解析】(1)设G为PC的中点,连接FG,EG,根据中位线定理得到FG ![]()
![]() CD,AE
CD,AE ![]()
![]() CD,进而可得到AF∥GE,再由线面平行的判定定理可证明AF∥平面PCE,得证.(2)根据PA=AD=2可得到AF⊥PD,再由线面垂直的性质定理可得到PA⊥CD,然后由AD⊥CD结合线面垂直的判定定理得到CD⊥平面PAD,同样得到GE⊥平面PCD,再由面面垂直的判定定理可得证.(3)先由(2)可得知EG为四面体PEFC的高,进而求出S△PCF , 根据棱锥的体积公式可得到答案.
CD,进而可得到AF∥GE,再由线面平行的判定定理可证明AF∥平面PCE,得证.(2)根据PA=AD=2可得到AF⊥PD,再由线面垂直的性质定理可得到PA⊥CD,然后由AD⊥CD结合线面垂直的判定定理得到CD⊥平面PAD,同样得到GE⊥平面PCD,再由面面垂直的判定定理可得证.(3)先由(2)可得知EG为四面体PEFC的高,进而求出S△PCF , 根据棱锥的体积公式可得到答案.
【考点精析】本题主要考查了棱锥的结构特征和直线与平面平行的判定的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=3,an+1=can+m(c,m为常数)
(1)当c=1,m=1时,求数列{an}的通项公式an;
(2)当c=2,m=﹣1时,证明:数列{an﹣1}为等比数列;
(3)在(2)的条件下,记bn= ![]() ,Sn=b1+b2+…+bn , 证明:Sn<1.
,Sn=b1+b2+…+bn , 证明:Sn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年10月,继微信支付对提现转账收费后,支付宝也开始对提现转账收费,随着这两大目前用户使用粘度最高的第三方支付开始收费,业内人士分析,部分对价格敏感的用户或将回流至传统银行体系,某调查机构对此进行调查,并从参与调查的数万名支付宝用户中随机选取200人,把这200人分为3类:认为使用支付宝方便,仍使用支付宝提现转账的用户称为“![]() 类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“
类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“![]() 类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“
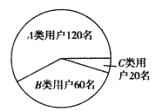
类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“![]() 类用户”,各类用户的人数如图所示:
类用户”,各类用户的人数如图所示:
同时把这200人按年龄分为青年人组与中老年人组,制成如图所示的![]() 列联表:
列联表:
| 非 | 合计 | |
青年 | 20 | ||
中老年 | 40 | ||
合计 | 200 |
(Ⅰ)完成![]() 列联表并判断是否有99.5%的把握认为“
列联表并判断是否有99.5%的把握认为“![]() 类用户与年龄有关”;
类用户与年龄有关”;
(Ⅱ)从这200人中按![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中
类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户均存在的概率;
类用户均存在的概率;
(Ⅲ)把频率作为概率,从支付宝所有用户(人数很多)中随机抽取3人,用![]() 表示所选3人中
表示所选3人中![]() 类用户的人数,求
类用户的人数,求![]() 的分布列与期望.
的分布列与期望.
附:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求点![]() 的直角坐标,并求曲线
的直角坐标,并求曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 的两个交点为
的两个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生产甲乙两种元件,其质量按检测指标划分为:指标大于或者等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
元件甲 | 8 | 12 | 40 | 32 | 8 |
元件乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件甲、乙为正品的概率;
(2)生产一件元件甲,若是正品可盈利40元,若是次品则亏损5元,生产一件元件乙,若是正品可盈利50元,若是次品则亏损10元.在(1)的前提下:
(i)记![]() 为生产1件甲和1件乙所得的总利润,求随机变量
为生产1件甲和1件乙所得的总利润,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5件元件乙所获得的利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
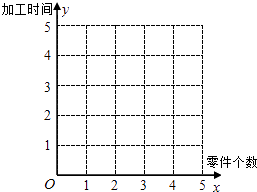
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线 ![]() =bx+a,其中b=
=bx+a,其中b= 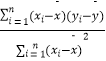 =
= 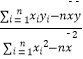 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com