
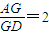 ;空间中:在正四面体ABCD中,若三角形BCD中心为M,正四面体ABCD中心为O,则
;空间中:在正四面体ABCD中,若三角形BCD中心为M,正四面体ABCD中心为O,则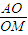 = .
= .  中的结论是二维线段长与线段长的关系,类比后的结论应该为三维的边与边的关系.
中的结论是二维线段长与线段长的关系,类比后的结论应该为三维的边与边的关系.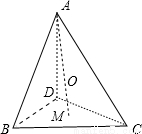 解:由平面图形的性质类比猜想空间几何体的性质,
解:由平面图形的性质类比猜想空间几何体的性质,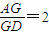 ”,
”,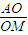 =3.”
=3.”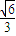 ,又O到四面体各面的距离都相等,
,又O到四面体各面的距离都相等,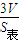 ,可求得r即OM=
,可求得r即OM=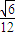 ,
,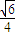 ,所以
,所以 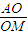 =3.
=3.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014届吉林省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
A.1:2 B.1:4 C.1:6 D.1:8
查看答案和解析>>
科目:高中数学 来源:2012届云南省高二下学期期中考试文科数学试题 题型:选择题
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
A.1:2 B. 1:4 C. 1:6 D. 1:8
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1:4 | B.1:6 | C.1:8 | D.1:9 |
查看答案和解析>>
科目:高中数学 来源:2010年浙江省嘉兴市高考数学一模试卷(理科)(解析版) 题型:选择题
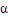 上,已知它的底面边长为2,高h,边BC在平面上转动,若某个时刻它在平面
上,已知它的底面边长为2,高h,边BC在平面上转动,若某个时刻它在平面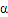 上的射影是等腰直角三角形,则h的取值范围是( )
上的射影是等腰直角三角形,则h的取值范围是( )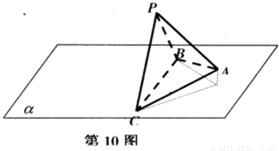
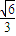 ]
]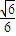 ]
]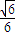 ]∪[
]∪[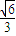 ,1]
,1]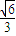 ]∪(
]∪(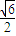 ,1)
,1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com