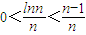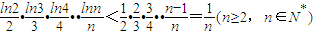【答案】
分析:利用导数求函数的单调区间的步骤是①求导函数f′(x);②解f′(x)>0(或<0);③得到函数的增区间(或减区间),
对于本题的(1)在求单调区间时要注意函数的定义域以及对参数a的讨论情况;
(2)点(2,f(2))处的切线的倾斜角为45°,即切线斜率为1,即f'(2)=1,可求a值,代入得g(x)的解析式,由t∈[1,2],且g(x)在区间(t,3)上总不是单调函数可知:
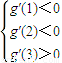
,于是可求m的范围.
(3)是近年来高考考查的热点问题,即与函数结合证明不等式问题,常用的解题思路是利用前面的结论构造函数,利用函数的单调性,对于函数取单调区间上的正整数自变量n有某些结论成立,进而解答出这类不等式问题的解.
解答:解:(Ⅰ)
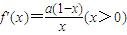
(2分)
当a>0时,f(x)的单调增区间为(0,1],减区间为[1,+∞);
当a<0时,f(x)的单调增区间为[1,+∞),减区间为(0,1];
当a=0时,f(x)不是单调函数(4分)
(Ⅱ)
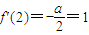
得a=-2,f(x)=-2lnx+2x-3
∴
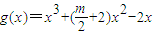
,
∴g'(x)=3x
2+(m+4)x-2(6分)
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2
∴
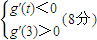
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
所以有:
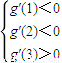
,∴
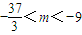
(10分)
(Ⅲ)令a=-1此时f(x)=-lnx+x-3,所以f(1)=-2,
由(Ⅰ)知f(x)=-lnx+x-3在(1,+∞)上单调递增,
∴当x∈(1,+∞)时f(x)>f(1),即-lnx+x-1>0,
∴lnx<x-1对一切x∈(1,+∞)成立,(12分)
∵n≥2,n∈N*,则有0<lnn<n-1,
∴
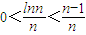
∴
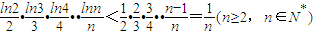 点评:
点评:本题考查利用函数的导数来求函数的单调区间,已知函数曲线上一点求曲线的切线方程即对函数导数的几何意义的考查,考查求导公式的掌握情况.含参数的数学问题的处理,构造函数求解证明不等式问题.

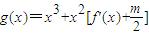 在区间(t,3)上总不是单调函数,求m的取值范围;
在区间(t,3)上总不是单调函数,求m的取值范围;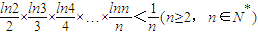 .
.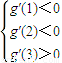 ,于是可求m的范围.
,于是可求m的范围.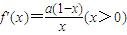 (2分)
(2分)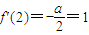 得a=-2,f(x)=-2lnx+2x-3
得a=-2,f(x)=-2lnx+2x-3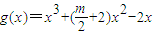 ,
,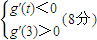
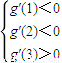 ,∴
,∴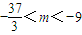 (10分)
(10分)