
【题目】已知函数 ![]() ,
, ![]() .
.
(1)若函数 ![]() 在
在 ![]() 上是减函数,求实数
上是减函数,求实数 ![]() 的取值范围;
的取值范围;
(2)是否存在整数 ![]() ,使得
,使得 ![]() 的解集恰好是
的解集恰好是 ![]() ,若存在,求出
,若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(1)解:令 ![]() ,则
,则 ![]() .
.
当 ![]() ,即
,即 ![]() 时,
时, ![]() 恒成立,
恒成立,
所以 ![]() .
.
因为 ![]() 在
在 ![]() 上是减函数,
上是减函数,
所以 ![]() ,解得
,解得 ![]() ,
,
所以 ![]() .
.
由 ![]() ,解得
,解得 ![]() 或
或 ![]() .
.
当 ![]() 时,
时, ![]() 的图象对称轴
的图象对称轴 ![]() ,
,
且方程 ![]() 的两根均为正,
的两根均为正,
此时 ![]() 在
在 ![]() 为减函数,所以
为减函数,所以 ![]() 符合条件.
符合条件.
当 ![]() 时,
时, ![]() 的图象对称轴
的图象对称轴 ![]() ,
,
且方程 ![]() 的根为一正一负,
的根为一正一负,
要使 ![]() 在
在 ![]() 单调递减,则
单调递减,则 ![]() ,解得
,解得 ![]() .
.
综上可知,实数 ![]() 的取值范围为
的取值范围为 ![]()
(2)解:假设存在整数 ![]() ,使
,使 ![]() 的解集恰好是
的解集恰好是 ![]() ,则
,则
①若函数 ![]() 在
在 ![]() 上单调递增,则
上单调递增,则 ![]() ,
, ![]() 且
且 ![]() ,
,
即 ![]()
作差得到 ![]() ,代回得到:
,代回得到: ![]() ,即
,即 ![]() ,由于
,由于 ![]() 均为整数,
均为整数,
故 ![]() ,
, ![]() ,
, ![]() 或
或 ![]() ,
, ![]() ,
, ![]() ,经检验均不满足要求;
,经检验均不满足要求;
②若函数 ![]() 在
在 ![]() 上单调递减,则
上单调递减,则 ![]() ,
, ![]() 且
且 ![]() ,
,
即 ![]()
作差得到 ![]() ,代回得到:
,代回得到: ![]() ,即
,即 ![]() ,由于
,由于 ![]() 均为整数,
均为整数,
故 ![]() ,
, ![]() ,
, ![]() 或
或 ![]() ,
, ![]() ,
, ![]() ,经检验均不满足要求;
,经检验均不满足要求;
③若函数 ![]() 在
在 ![]() 上不单调,则
上不单调,则 ![]() ,
, ![]() 且
且 ![]() ,
,
即 ![]() 作差得到
作差得到 ![]() ,代回得到:
,代回得到: ![]() ,即
,即 ![]() ,由于
,由于 ![]() 均为整数,
均为整数,
故 ![]() ,
, ![]() ,
, ![]() 或
或 ![]() ,
, ![]() ,
, ![]() ,,经检验均满足要求;
,,经检验均满足要求;
综上:符合要求的整数 ![]() 、
、 ![]() 是
是 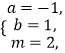 或
或 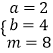
【解析】(1)首先求出对称轴根据题意分情况讨论区间在对称轴的右边,且f(0)不小于0以及区间在对称轴的左边,且f(0)不大于0,分别解出两种情况下的m的取值范围即可。(2)根据题意假设存在整数a、b使得 a ≤ f ( x ) ≤ b 的解集恰好是 [ a , b ] ,则 f ( a ) = a , f ( b ) = b,代入数值求出a、b的值再代入到不等式检验即可。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式 ![]() 的解集为( )
的解集为( )
A.(﹣1,0)∪(1,+∞)
B.(﹣∞,﹣1)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是定义在
是定义在 ![]() 上的奇函数,且
上的奇函数,且  偶函数
偶函数 ![]() 的定义域为
的定义域为 ![]() ,且当
,且当 ![]() 时,
时, ![]() .若存在实数
.若存在实数 ![]() ,使得
,使得 ![]() 成立,则实数
成立,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“p∨q”是“p∧q”的充分不必要条件
B.样本10,6,8,5,6的标准差是3.3
C.K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关
D.设有一个回归直线方程为 ![]() =2﹣1.5x,则变量x每增加一个单位,
=2﹣1.5x,则变量x每增加一个单位, ![]() 平均减少1.5个单位.
平均减少1.5个单位.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 直径,
直径, ![]() 所在的平面,
所在的平面, ![]() 是圆周上不同于
是圆周上不同于 ![]() 的动点.
的动点.
(1)证明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() ,且当二面角
,且当二面角 ![]() 的正切值为
的正切值为 ![]() 时,求直线
时,求直线 ![]() 与平面
与平面 ![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2+x>0},集合B= ![]() ,则(UA)∪B=( )
,则(UA)∪B=( )
A.[0,2)
B.[﹣1,0]
C.[﹣1,2)
D.(﹣∞,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x3﹣(1+
x3﹣(1+ ![]() )x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
)x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
A.![]() b2﹣
b2﹣ ![]() b3
b3
B.![]() b﹣
b﹣ ![]()
C.0
D.2b﹣ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com