
【题目】
如图所示多面体中,AD⊥平面PDC,ABCD为平行四边形,E,F分别为AD,BP的中点,AD=![]() ,AP=
,AP=![]() ,PC=
,PC=![]() .
.
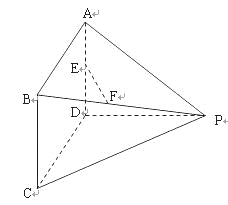
(Ⅰ)求证:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求证BE⊥DP;
(Ⅲ)若∠CDP=120°,求该多面体的体积.
【答案】(1)、(2)见解析;(3)![]() .
.
【解析】
(Ⅰ)取PC的中点为O,连FO,DO,
∵F,O分别为BP,PC的中点,
∴![]() ∥BC,且
∥BC,且![]() ,
,
又ABCD为平行四边形,![]() ∥BC,且
∥BC,且![]() ,
,
∴![]() ∥ED,且
∥ED,且![]()
∴四边形EFOD是平行四边形
即EF∥DO又EF![]() 平面PDC
平面PDC
∴EF∥平面PDC.
(Ⅱ)若∠CDP=90°,则PD⊥DC,
又AD⊥平面PDC∴AD⊥DP,
∴PD⊥平面ABCD,
∵BE![]() 平面ABCD,
平面ABCD,
∴BE⊥DP
(Ⅲ)连结AC,由ABCD为平行四边形可知![]() 与
与![]() 面积相等,
面积相等,
所以三棱锥![]() 与三棱锥
与三棱锥![]() 体积相等,
体积相等,
即五面体的体积为三棱锥![]() 体积的二倍.
体积的二倍.
∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4
又∠CDP=120°PC=2![]() ,
,
由余弦定理并整理得![]() , 解得DC=2
, 解得DC=2
∴![]() 三棱锥
三棱锥![]() 的体积
的体积![]()
∴该五面体的体积为![]()


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图茎叶图:

![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
![]() 完成下面的列联表,并根据列联表判断是否有
完成下面的列联表,并根据列联表判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | |
第一阶段 | ||
第二阶段 |
附:![]()
|
|
|
|
k |
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )

A. 22种 B. 24种 C. 25种 D. 27种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() 是坐标原点,若
是坐标原点,若![]() ,且
,且![]() 方向是沿
方向是沿![]() 的方向绕着
的方向绕着![]() 点按逆时针方向旋转
点按逆时针方向旋转![]() 角得到的,则称
角得到的,则称![]() 经过一次
经过一次![]() 变换得到
变换得到![]() ,现有向量
,现有向量![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,
,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,…,如此下去,
,…,如此下去,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,设
,设![]() ,
,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.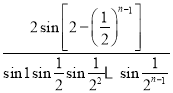 B.
B.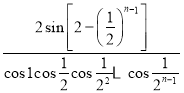
C.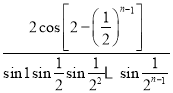 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)
等边△ABC的边长为3,点D,E分别为AB,AC上的点,且满足![]() (如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
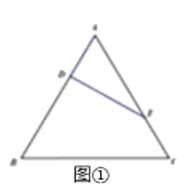
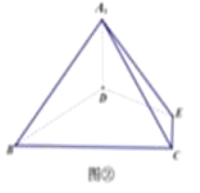
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P(不包括端点),使直线PA1与平面A1BD所成的角为60°?若存在,求出A1P的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】故宫博物院五一期间同时举办“戏曲文化展”、“明代御窖瓷器展”、“历代青绿山水画展”、 “赵孟頫书画展”四个展览.某同学决定在五一当天的上、下午各参观其中的一个,且至少参观一个画展,则不同的参观方案共有
A. 6种 B. 8种 C. 10种 D. 12种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 在
在![]() 的单调区间;
的单调区间;
(Ⅱ)方程![]() 有3个不同的实根,求实数
有3个不同的实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若对于任意的
时,若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求满足条件的正整数
,求满足条件的正整数![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,CM⊥AB,垂足为M,且AE=AC=2![]() ,BD=2BC=4,
,BD=2BC=4,
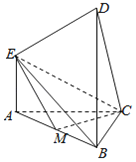
(1)求证:CM⊥ME;
(2)求二面角A﹣MC﹣E的余弦值.
(3)在线段DC上是否存在一点N,使得直线BN∥平面EMC,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com