
用直线y=m和直线y=x将区域x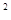 +y
+y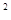
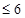 分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
A.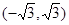 | B.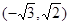 | C. | D.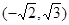 |
A
解析考点:排列、组合的实际应用.
分析:由题意知Y=X与X=m两直线的交点必在Y=X这条直线上,而要想使任意两块不同色共有涂法120种,必须让直线X=m,Y=X将圆分成四块不同的面积,那么不同的涂法是5×4×3×2,要求出Y=X与圆的交点,得到结果.
解:由题意知Y=X与X=m两直线的交点必在Y=X这条直线上,
而要想使任意两块不同色共有涂法120种,
∴必须让直线X=m,Y=X将圆分成四块不同的面积,
那么不同的涂法才能是5×4×3×2=120.
要求出Y=X与圆的交点分别为(-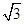 ,-
,-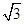 )(
)(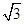 ,
,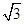 ).
).
∴-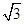 ≤m≤
≤m≤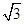 ,
,
∵当m=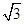 或-
或-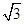 时,两直线只能把该圆分成三个区域,
时,两直线只能把该圆分成三个区域,
∴不成立,
∴-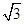 <m<
<m<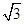 .
.
故答案为:A


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011年河北省石家庄市高三第一次模拟考试数学试卷文科 题型:选择题
用直线y=m和直线y=x将区域x +y
+y
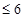 分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
A.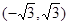 B.
B.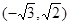 C.
C.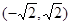 D.
D.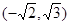
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.(-
| B.(-
| C.(-
| D.(-
|
查看答案和解析>>
科目:高中数学 来源:《计数原理》2013年广东省广州大学附中高考数学二轮复习检测(解析版) 题型:选择题
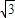 ,
,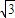 )
)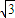 ,
,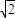 )
)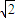 ,
,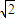 )
)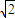 ,
,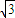 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com