
【题目】已知圆![]() :
:![]() ,圆
,圆![]() 与圆
与圆![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
(1)求圆![]() 的方程;
的方程;
(2)过直线![]() 上的点
上的点![]() 分别作斜率为
分别作斜率为![]() ,4的两条直线
,4的两条直线![]() ,
,![]() ,求使得
,求使得![]() 被圆
被圆![]() 截得的弦长与
截得的弦长与![]() 被圆
被圆![]() 截得的弦长相等时点
截得的弦长相等时点![]() 的坐标.
的坐标.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() ,斜率为1的直线与抛物线
,斜率为1的直线与抛物线![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作直线交抛物线
作直线交抛物线![]() 于不同于
于不同于![]() 的两点
的两点![]() 、
、![]() ,若直线
,若直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() 两点,求
两点,求![]() 取最小值时直线
取最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 为椭圆
为椭圆![]() 的左顶点,过
的左顶点,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 的中点.
的中点.
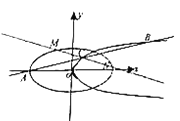
(1)求证:点![]() 的横坐标是定值,并求出该定值;
的横坐标是定值,并求出该定值;
(2)若直线![]() 过
过![]() 点,且倾斜角和直线
点,且倾斜角和直线![]() 的倾斜角互补,交椭圆于
的倾斜角互补,交椭圆于![]() 、
、![]() 两点,求
两点,求![]() 的值,使得
的值,使得![]() 的面积最大.
的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
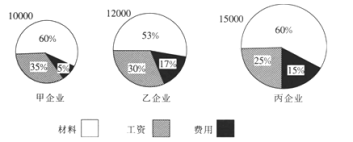
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个三角形数表按如下方式构成(如图:其中项数![]() ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:![]() ;
;![]() 为数表中第
为数表中第![]() 行的第
行的第![]() 个数.
个数.
![]()
![]() …
…![]()
![]()
![]()
![]() …
…![]()
![]() …
…![]()
……
![]()
(1)求第2行和第3行的通项公式![]() 和
和![]() ;
;
(2)证明:数表中除最后2行外每一行的数都依次成等差数列,并求![]() 关于
关于![]() 的表达式;
的表达式;
(3)若![]() ,
,![]() ,试求一个等比数列
,试求一个等比数列![]() ,使得
,使得![]() ,且对于任意的
,且对于任意的![]() ,均存在实数
,均存在实数![]() ,当
,当![]() 时,都有
时,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的序号是( )
①函数f(x)在定义域R内可导,“f′(1)=0”是“函数f(x)在x=1处取极值”的充分不必要条件;
②函数f(x)=x3![]() ax在[1,2]上单调递增,则a≥﹣4
ax在[1,2]上单调递增,则a≥﹣4
③在一次射箭比赛中,甲、乙两名射箭手各射箭一次.设命题p:“甲射中十环”,命题q:“乙射中十环”,则命题“至少有一名射箭手没有射中十环”可表示为(¬p)∨(¬q);
④若椭圆![]() 左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
A.①③④B.②③④C.②③D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com