
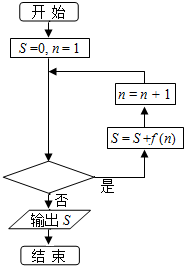
 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )| A. | n≤100? | B. | n≤99? | C. | n>100? | D. | n>99? |
分析 模拟程序框图的运行过程,找出此框图的算法功能,由条件S=10得出n的值,从而确定判断框内的条件.
解答 解:∵f(x)=$\frac{1}{\sqrt{x}+\sqrt{x-1}}$=$\sqrt{x}$-$\sqrt{x-1}$,
∴模拟程序框图的运行过程,得;
n=1时,S=0+f(1)=1,
n=2时,S=1+($\sqrt{2}$-1)=$\sqrt{2}$,
n=3时,S=$\sqrt{2}$+($\sqrt{3}$-$\sqrt{2}$)=$\sqrt{3}$,
以此类推,S=$\sqrt{n}$=10,
得n=100,
故判断框中应填“n≤100?”.
故选:A.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,是基础题目.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 球的体积与表面积之间的关系 | |
| B. | 正方形面积和它的边长之间的关系 | |
| C. | 家庭收入愈多,其消费支出也有增长的趋势 | |
| D. | 价格不变的条件下,商品销售额与销量量之间的关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2016)<0 | B. | f(2016)<e${\;}^{-201{6}^{2}}$ | ||
| C. | f(2)<0 | D. | f(2)>e-4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
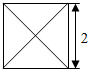 已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com