
(本题满分12分)
今年十一黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:
性别与对景区的服务是否满意 单位:名
| | 男 | 女 | 总计 |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
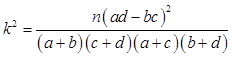
P(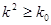 ) ) | 0.05 | 0.025 | 0.010 | 0.005 |
 | 3.841 | 5.024 | 6.635 | 7.879 |
解:(1)样本中满意的女游客为3名,样本中不满意的女游客为2名。
(2)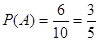 。
。
(3)有99%的把握认为:该景区游客性别与对景区的服务满意有关。
解析试题分析:(I)每个个体被抽取的概率为 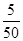 ,根据分层抽样,即可得样本中满意的女游客,样本中不满意的女游客的人数;
,根据分层抽样,即可得样本中满意的女游客,样本中不满意的女游客的人数;
(II)确定从这5名游客中随机选取两名的等可能事件的个数,其中事件A“选到满意与不满意的女游客各一名”包含6个基本事件,即可求得概率;
(III)由列联表,计算K2的值,根据P(K2>6.635)=0.010,即可得到结论.
解:(1)根据分层抽样可得:样本中满意的女游客为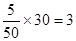 名,样本中不满意的女游客为
名,样本中不满意的女游客为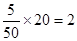 名。
名。
(2)记样本中对景区的服务满意的3名女游客分别为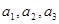 ,对景区的服务不满意的2名女游客分别为
,对景区的服务不满意的2名女游客分别为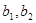 。从5名女游客中随机选取两名,共有10个基本事件,分别为:
。从5名女游客中随机选取两名,共有10个基本事件,分别为: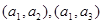 ,
,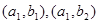 ,
,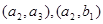 ,
,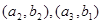 ,
,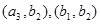 ;其中事件A:选到满意与不满意的女游客各一名包含了6个基本事件,分别为:
;其中事件A:选到满意与不满意的女游客各一名包含了6个基本事件,分别为: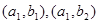 ,
,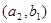
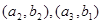 ,
,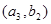
所以所求概率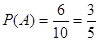 。
。
(3)假设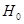 :该景区游客性别与对景区的服务满意无关,则
:该景区游客性别与对景区的服务满意无关,则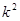 应该很小。
应该很小。
根据题目中列联表得: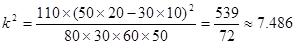
由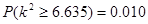 可知:有99%的把握认为:该景区游客性别与对景区的服务满意有关。
可知:有99%的把握认为:该景区游客性别与对景区的服务满意有关。
考点:本试题主要考查了分层抽样,考查等可能事件概率的求法,考查独立性检验知识,考查学生的计算能力,属于中档题.
点评:根据已知条件理解古典概型的概率中总的基本事件数从而求解概率的值,对于分层抽样的等概率抽样即为样本容量与总体的比值。


科目:高中数学 来源: 题型:解答题
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
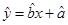 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。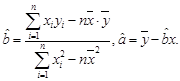 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
(Ⅰ)第二小组的频率是多少?样本容量是多少?
(Ⅱ)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?(Ⅲ)在这次测试中,学生跳绳次数的中位数、众数各是是多少?(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
以下是测得的某种产品的广告费支出x与销售额y(单位:百万元)之间,有如下的对应数据:
| 广告费支出x | 2 | 4 | 5 | 6 | 8 |
| 销售额y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
第26届世界大学生夏季运动会将于2011年8月12日至23日在深圳举行,为了搞好接待工作,组委会在某学院招募了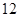 名男志愿者和
名男志愿者和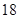 名女志愿者,调查发现,这
名女志愿者,调查发现,这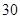 名志愿者的身高如下:(单位:cm )
名志愿者的身高如下:(单位:cm )
若身高在 cm以上(包括
cm以上(包括 cm)定义为“高个子”,身高在
cm)定义为“高个子”,身高在 cm以下定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
cm以下定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取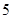 人,再从这
人,再从这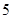 人中选
人中选 人,则至少有一人是“高个子”的概率是多少?
人,则至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选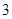 名志愿者,用
名志愿者,用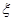 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出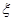 的分布列,并求
的分布列,并求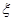 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2011年的自主招生考试成绩
中随机抽取100名学生的笔试成绩,按成绩
分组:第1组[75,80),第2组[80,85),
第3组[85,90),第4组[90,95),第5组
[95,100]得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组
中用分层抽样抽取6名学生进入第二轮面
试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.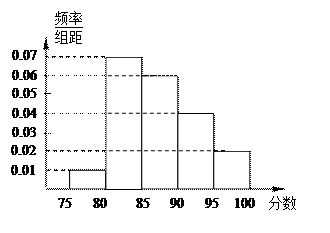
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某地区的一种传染病与饮用水的调查表:
| | 得病 | 不得病 | 合计 |
| 干净水 | 52 | 466 | 518 |
| 不干净水 | 94 | 218 | 312 |
| 合计 | 146 | 684 | 830 |
 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com