
【题目】定义域为R的奇函数f(x)满足f(4﹣x)+f(x)=0,当﹣2<x<0时,f(x)=2x , 则f(log220)=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:定义域为R的奇函数f(x)满足f(4﹣x)+f(x)=0,可得f(x)=﹣f(4﹣x)=f(x﹣4),所以函数的周期为:4.
当﹣2<x<0时,f(x)=2x ,
则f(log220)=f(log220﹣4)=f(log2 ![]() )=﹣f(﹣log2
)=﹣f(﹣log2 ![]() )=﹣
)=﹣ ![]() =﹣
=﹣ ![]() .
.
故选:B.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2. 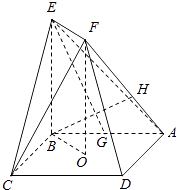
(1)求证:EG∥平面ADF;
(2)求二面角O﹣EF﹣C的正弦值;
(3)设H为线段AF上的点,且AH= ![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是![]() ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(1)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(2)这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)从6名同学中选4名同学组成一个代表队,参加4×400米接力比赛,问有多少种参赛方案?
(2)从6名同学中选4名同学参加场外啦啦队,问有多少种选法?
(3) 4名同学每人可从跳高、跳远、短跑三个项目中,任选一项参加比赛,问有多少种参赛方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数f(x)=2sinxcosx,x∈R的图象,只需将函数g(x)=2cos2x﹣1,x∈R的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南宋数学家秦九韶早在《数书九章》中就独立创造了已知三角形三边求其面积的公式:“以小斜幂并大斜幂,减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减之,以四约之,为实,一为从隅,开方得积.”(即:S=![]() ,a>b>c),并举例“问沙田一段,有三斜(边),其小斜一十三里,中斜一十四里,大斜一十五里,欲知为田几何?”则该三角形田面积为
,a>b>c),并举例“问沙田一段,有三斜(边),其小斜一十三里,中斜一十四里,大斜一十五里,欲知为田几何?”则该三角形田面积为
A. 82平方里 B. 84平方里
C. 85平方里 D. 83平方里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PC= ![]() AC,平面PAC⊥平面ABCD.
AC,平面PAC⊥平面ABCD. 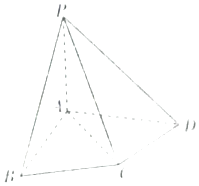
(1)点E在棱PC上,试确定点E的位置,使得PD⊥平面ABE;
(2)求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某厂生产某种产品的过程中记录的几组数据,其中![]() 表示产量(单位:吨),
表示产量(单位:吨),![]() 表示生产中消耗的煤的数量(单位:吨).
表示生产中消耗的煤的数量(单位:吨).
|
|
|
|
|
|
|
|
|
|
|
|
(1)试在给出的坐标系下作出散点图,根据散点图判断,在![]() 与
与![]() 中,哪一个方程更适合作为变量
中,哪一个方程更适合作为变量![]() 关于
关于![]() 的回归方程模型?(给出判断即可,不需要说明理由)
的回归方程模型?(给出判断即可,不需要说明理由)
(2)根据(1)的结果以及表中数据,建立变量![]() 关于
关于![]() 的回归方程.并估计生产
的回归方程.并估计生产![]() 吨产品需要准备多少吨煤.参考公式:
吨产品需要准备多少吨煤.参考公式: .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com