
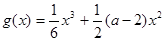 ,h(x)=2alnx,
,h(x)=2alnx,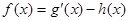 .
.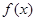 的单调性;
的单调性;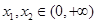 ,且
,且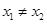 ,都有
,都有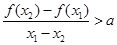
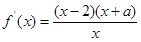
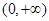 ,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点
,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点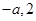 的大小,②注意根与定义域比较,所以
的大小,②注意根与定义域比较,所以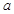 需和-2和0比较大小;(2)由对称性,不妨设
需和-2和0比较大小;(2)由对称性,不妨设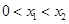 ,去分母得
,去分母得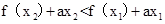 ,构造函数
,构造函数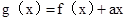 ,则其在定义域内单调递减,故
,则其在定义域内单调递减,故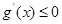 在
在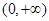 恒成立,而
恒成立,而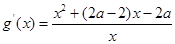 ,分子二次函数开口向上,不可能永远小于0,故不存在.
,分子二次函数开口向上,不可能永远小于0,故不存在.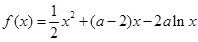 ,∴
,∴ 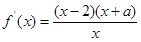 ,
, 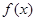 的定义域为
的定义域为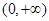 .
.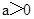 时,
时,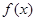 在
在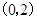 上是减函数,在在
上是减函数,在在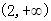 上是增函数;
上是增函数;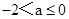 时,
时,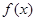 在
在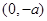 上是增函数;在
上是增函数;在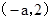 是是减函数;在
是是减函数;在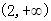 上是增函数;
上是增函数;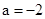 时,
时,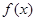 在
在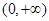 上是增函数;
上是增函数; 时,
时,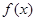 在
在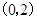 上是增函数;在
上是增函数;在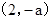 上是减函数;在
上是减函数;在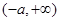 上是增函数.
上是增函数.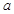 ,对任意的
,对任意的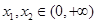 ,且
,且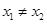 ,都有
,都有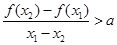 恒成立,不妨设
恒成立,不妨设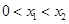 ,要使
,要使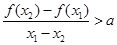 ,即
,即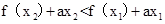 .
.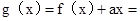
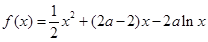 ,只要
,只要 在
在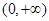 为减函数.
为减函数.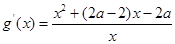 ,由题意
,由题意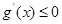 在
在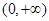 上恒成立,得
上恒成立,得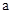 不存在.
不存在. 

 全能测控一本好卷系列答案
全能测控一本好卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com