
【题目】已知函数f(x)=|x﹣a|+2a,且不等式f(x)≤4的解集为{x|﹣1≤x≤3}.
(1)求实数a的值.
(2)若存在实数x0,使f(x0)≤5m2+m﹣f(﹣x0)成立,求实数m的取值范围.
【答案】(1)a=1(2)(﹣∞,![]() ]∪[1,+∞)
]∪[1,+∞)
【解析】
(1)解不等式f(x)≤4,根据其解集,得到![]() 的值;(2)将所求不等式转化为5m2+m≥[f(x)+f(﹣x)]min,得到f(x)+f(﹣x)的最小值,从而得到关于
的值;(2)将所求不等式转化为5m2+m≥[f(x)+f(﹣x)]min,得到f(x)+f(﹣x)的最小值,从而得到关于![]() 的不等式,解出
的不等式,解出![]() 的取值范围.
的取值范围.
(1)由f(x)=|x﹣a|+2a≤4,得2a﹣4≤x﹣a≤﹣2a+4,
∴3a﹣4≤x≤﹣a+4,
∵不等式f(x)≤4的解集为{x|﹣1≤x≤3},
∴![]() ,∴a=1;
,∴a=1;
(2)由(1)知f(x)=|x﹣1|+2,
∵存在实数x0,使f(x0)≤5m2+m﹣f(﹣x0)成立,
∴只需5m2+m≥[f(x)+f(﹣x)]min
∵f(x)+f(﹣x)=|x﹣1|+|x+1|+4≥|(x﹣1)﹣(x+1)|+4=6,
当且仅当(x﹣1)(x+1)≤0,即﹣1≤x≤1时取等号,
∴5m2+m≥6,
∴![]() 或m≥1,
或m≥1,
∴m的取值范围为(﹣∞,![]() ]∪[1,+∞).
]∪[1,+∞).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 为斜边
为斜边![]() 的中点,且
的中点,且![]() 平行于
平行于![]() 轴.
轴.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() .以
.以![]() 为直径的圆交
为直径的圆交![]() 轴于
轴于![]() 即此圆的圆心为
即此圆的圆心为![]() ,
,![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
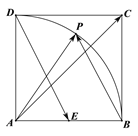
【题目】如图,在边长为1的正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧(在正方形内,包括边界点)上的任意一点,则![]() 的取值范围是________; 若向量
的取值范围是________; 若向量![]() ,则
,则![]() 的最小值为_________.
的最小值为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 为焦点是
为焦点是![]() 的抛物线上一点,
的抛物线上一点, ![]() 为直线
为直线![]() 上任一点,
上任一点, ![]() 分别为椭圆
分别为椭圆![]() 的上,下顶点,且
的上,下顶点,且![]() 三点的连线可以构成三角形.
三点的连线可以构成三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点分别交于点
的另一交点分别交于点![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品每千克定价10元,商家采取了如下的促销方式:
一次购买量 | 促销方式 |
不多于20千克 | 原价出售 |
多于20千克且不多于40千克 | 不多于20千克部分,原价出售 多于20千克部分,九折出售 |
多于40千克 | 不多于20千克部分,原价出售 多于20千克且不多于40千克部分,九折出售 多于40千克部分八折出售 |
(1)求一次购买![]() (单位:千克),此商品的花费
(单位:千克),此商品的花费![]() (单位:元)的函数解析式;
(单位:元)的函数解析式;
(2)某人一次购买此商品400元,问他能购得此商品多少千克?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() 设圆C的半径为1,圆心在直线l上.
设圆C的半径为1,圆心在直线l上.
(1)若圆心C也在直线![]() 上,过点
上,过点![]() 作圆C的切线,求切线的方程;
作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使得![]() ,求圆心C的横坐标
,求圆心C的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形。
都为矩形。

(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论。
?请证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com