
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量(单位:克)分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,经统计得频率分布直方图如图所示.
中,经统计得频率分布直方图如图所示.

(1)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在![]() 内的概率;
内的概率;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
![]() 方案:所有芒果以10元/千克收购;
方案:所有芒果以10元/千克收购;
![]() 方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
通过计算确定种植园选择哪种方案获利更多?
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对某乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量![]() 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费![]() 万元之间的函数关系为
万元之间的函数关系为![]() (其中推广促销费不能超过5千元).已知加工此农产品还要投入成本
(其中推广促销费不能超过5千元).已知加工此农产品还要投入成本![]() 万元(不包括推广促销费用),若加工后的每件成品的销售价格定为
万元(不包括推广促销费用),若加工后的每件成品的销售价格定为![]() 元/件.
元/件.
(1)试将该批产品的利润![]() 万元表示为推广促销费
万元表示为推广促销费![]() 万元的函数;(利润=销售额-成本-推广促销费)
万元的函数;(利润=销售额-成本-推广促销费)
(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a≥3,函数F(x)=min{2|x﹣1|,x2﹣2ax+4a﹣2},其中min(p,q)= ![]()
(1)求使得等式F(x)=x2﹣2ax+4a﹣2成立的x的取值范围
(2)(i)求F(x)的最小值m(a)
(ii)求F(x)在[0,6]上的最大值M(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程;曲线
的直角坐标方程;曲线![]() 的极坐标方程。
的极坐标方程。
(2)当曲线![]() 与曲线
与曲线![]() 有两个公共点时,求实数
有两个公共点时,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,在收费10元的基础上,每超过
的包裹,在收费10元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司将最近承揽的100件包裹的重量统计如下:

公司对近60天,每天揽件数量统计如下表:

以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,其余的用作其他费用.目前前台有工作人员3人,每人每天揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是决策者,是否裁减工作人员1人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月9日,教育部考试中心下发了《关于![]() 年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了
年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.鞍山市教育部门积极回应,编辑传统文化教材,在全是范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了![]() 位市民进行了解,发现支持开展的占
位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民
,在抽取的男性市民![]() 人中支持态度的为
人中支持态度的为![]() 人.
人.
支持 | 不支持 | 合计 | |
男性 | |||
女性 | |||
合计 |
(1)完成![]() 列联表
列联表
(2)判断是否有![]() 的把握认为性别与支持有关?
的把握认为性别与支持有关?
附:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率
的离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
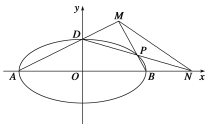
(2)如图所示,A、B、D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M,设BP的斜率为k,MN的斜率为m.证明:2m-k为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com