
【题目】已知函数 ![]()
(1)判断f(x)的单调性,说明理由.
(2)解方程f(2x)=f﹣1(x).
【答案】
(1)解:4x﹣1>0,所以x>0,所以定义域是(0,+∞),f(x)在(0,+∞)上单调增.
证法一:设0<x1<x2,则 ![]() =
= ![]()
又∵0<x1<x2,∴ ![]() ,
, ![]()
∴ ![]() ,即
,即 ![]()
∴f(x1)<f(x2),f(x)在(0,+∞)上单调增.
证法二:∵y=log4x在(0,+∞)上都是增函数,
y=4x﹣1在(0,+∞)上是增函数且y=4x﹣1>0
∴ ![]() 在(0,+∞)上也是增函数
在(0,+∞)上也是增函数
(2)解: ![]() ,
,
∴f(2x)=f﹣1(x),即0<42x﹣1=4x+142x﹣4x﹣2=0,解得4x=﹣1(舍去)或4x=2,
∴ ![]()
经检验, ![]() 是方程的根
是方程的根
【解析】(1)利用函数单调性的定义,或复合函数单调性的判定方法,可得结论;(2)求出f﹣1(x),可得方程,解方程,即可得到结论.
【考点精析】解答此题的关键在于理解复合函数单调性的判断方法的相关知识,掌握复合函数f[g(x)]的单调性与构成它的函数u=g(x),y=f(u)的单调性密切相关,其规律:“同增异减”,以及对函数的零点的理解,了解函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.


科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.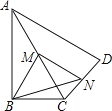
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考浙江文数】如图,设抛物线![]() 的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.
的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.
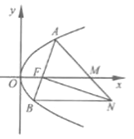
(I)求p的值;
(II)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x
轴交于点M.求M的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= ![]() acosB. (Ⅰ)求角B的大小;
acosB. (Ⅰ)求角B的大小;
(Ⅱ)若b=3,sinC=2sinA,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【天津市红桥区重点中学八校2017届高三4月联考数学(文)】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点
的焦点
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点, ![]() ,
, ![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.①若直线
两侧的动点.①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() ,
, ![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由
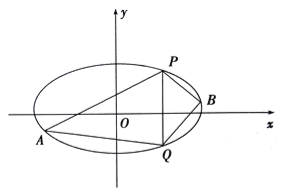
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2015高考福建文数】全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 | | 2 |
2 | | 8 |
3 | | 7 |
4 | | 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是梯形.四边形
是梯形.四边形![]() 是矩形.且平面
是矩形.且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的动点.
上的动点.
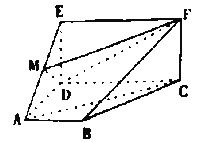
(Ⅰ)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com