已知函数f(x)=x2-2ax-3a2.
(1)若a=1,求函数f(x)的值域;
(2)当x∈[1,4]时,求f(x)的最小值;
(3)是否存在实数a,对于任意x∈[1,4],f(x)≥-4a恒成立?若存在,求实数a的取值范围;若不存在,说明理由.
解:(1)∵a=1,∴函数f(x)=x
2-2ax-3a
2=x
2-2x-3=(x-1)
2-4≥-4,
∴函数的值域为[-4,+∞).
(2)函数f(x)=x
2-2ax-3a
2=(x-a)
2-4a
2,对称轴为x=a.
当a<1时,在区间[1,4]上函数单调递增,∴函数f(x)最小值为f(1)=1-2a-3a
2;
当1≤a≤4时,函数f(x)在[1,a]上单调递减,在[a,4]上单调递增,∴函数f(x)最小值为f(a)=-4a
2;
当a>4时,在区间[1,4]上函数单调递减,∴函数f(x)最小值为f(4)=16-8a-3a
2;
(3)对于任意x∈[1,4],f(x)≥-4a恒成立,等价于对于任意x∈[1,4],f(x)
min≥-4a恒成立
由(2)知,
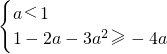
或
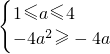
或
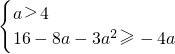
∴
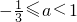
或a=1
∴
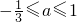
.
分析:(1)把二次函数f(x)的解析式配方,利用配方法求函数的值域.
(2)配方,确定函数的对称轴,根据区间[1,4],分类讨论,可求函数f(x)最小值;
(3)对于任意x∈[1,4],f(x)≥-4a恒成立,等价于对于任意x∈[1,4],f(x)
min≥-4a恒成立,故可求实数a的取值范围.
点评:本题考查求二次函数在闭区间上的值域,函数的恒成立问题,考查分类讨论的数学思想,属于中档题.

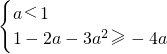 或
或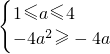 或
或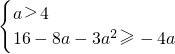
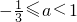 或a=1
或a=1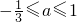 .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<