已知f(x)是定义在R上的函数,且满足下列条件:
①对任意的x、y∈R,f(x+y)=f(x)+f(y);
②当x>0时,f(x)<0.
(1)证明f(x)在R上是减函数;
(2)在整数集合内,关于x的不等式f(x2-4)-f(2x-2a)>f(0)的解集为{1},求实数a的取值范围.
【答案】
分析:(1)首先取x=y=0,得f(0)=f(0)+f(0),得f(0)=0,令y=-x,再取y=-x,可以证出f(-x)=-f(x),得函数f(x)在R上是奇函数,最后可以用定义证出f(x)在R上是减函数;
(2)原不等式等价于:x
2-4<2x-2a即x
2-2x+2a-4<0,设其左边为函数g(x)=x
2-2x+2a-4,通过讨论函数值
g(0),g(1)和g(2)的正负,建立不等式组,可解出实数a的取值范围.
解答:解:(1)当时x=y=0,f(0)=f(0)+f(0),
得f(0)=0,令y=-x,则f(0)=f(x)+f(-x)
∴f(-x)=-f(x)∴f(x)在R上是奇函数,
设x
1>x
2,则f(x
1)-f(x
2)=f(x
1)+f(-x
2)
=f(x
1-x
2)<0
∴f(x
1)<f(x
2),
∴f(x)在R上是减函数(6分)
(2)f(x
2-4)-f(2x-2a)>f(0)等价于
x
2-4<2x-2a即x
2-2x+2a-4<0(8分)
令g(x)=x
2-2x+2a-4
根据题意,

的实数a的取值范围为
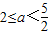
∴
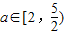
(12分)
点评:本题考查了函数的单调性与奇偶性的判断与证明,及其一元二次方程与二次函数关系等知识点,属于中档题.

 的实数a的取值范围为
的实数a的取值范围为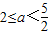
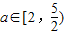 (12分)
(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案