
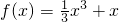 ,x∈R,如果至少存在一个实数x,使f (a-x)+f (ax2-1)<0,成立,则实数a的取值范围为
,x∈R,如果至少存在一个实数x,使f (a-x)+f (ax2-1)<0,成立,则实数a的取值范围为 ,+∞)
,+∞) ]
] )
) )∪(-
)∪(- ,-1)
,-1)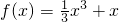 ,得f′(x)=x2+1>0,所以f(x)是增函数,且易知为奇函数.
,得f′(x)=x2+1>0,所以f(x)是增函数,且易知为奇函数. ,解得a≥
,解得a≥ .
. ).
).

科目:高中数学 来源:专项题 题型:解答题
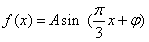 ,x∈R,A>0,
,x∈R,A>0,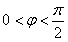 。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。
。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。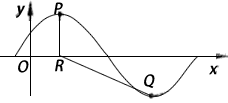
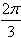 ,求A的值。
,求A的值。查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省永州市祁阳四中高三(上)段考数学试卷(文科)(解析版) 题型:解答题
 已知函数
已知函数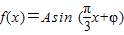 ,x∈R,A>0,
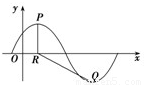
,x∈R,A>0,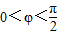 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).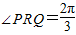 ,求A的值.
,求A的值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省德兴一中、横峰中学、铅山一中、弋阳一中四校联考高二(下)期中数学试卷(文科)(解析版) 题型:解答题
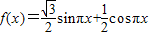 ,x∈R.
,x∈R.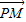 与
与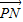 的夹角的余弦.
的夹角的余弦.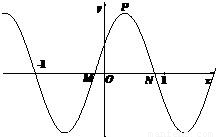
查看答案和解析>>
科目:高中数学 来源:2011年福建省福州市高三3月质量检查数学试卷(理科)(解析版) 题型:解答题
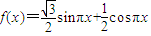 ,x∈R.
,x∈R.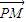 与
与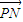 的夹角的余弦.
的夹角的余弦.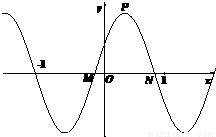
查看答案和解析>>
科目:高中数学 来源:2011年福建省福州市高三3月质量检查数学试卷(文科)(解析版) 题型:解答题
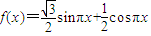 ,x∈R.
,x∈R.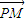 与
与 的夹角的余弦.
的夹角的余弦.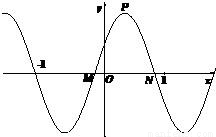
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com