
 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.分析 (1)连结OP,推导出OP⊥AB,从而OP⊥平面ABCD,由OP⊥OD,OP⊥OC,得OD⊥OC,再由OP⊥OC,能证明OC⊥PD.
(2)设AD=1,则AB=2,推导出∠DPA为直线PD与平面PAB所成的角,设PC的中点为M,连接DM,则DM⊥PC在Rt△CBP中,过M作NM⊥PC,交PB于点N,则∠DMN为二面角D-PC-B的一个平面角,由此能求出二面角D-PC-B的余弦值.
解答 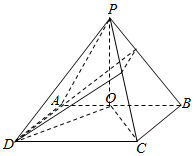 证明:(1)连结OP,∵PA=PB,O为AB的中点,∴OP⊥AB.
证明:(1)连结OP,∵PA=PB,O为AB的中点,∴OP⊥AB.
∵侧面PAB⊥底面ABCD,∴OP⊥平面ABCD,
∴OP⊥OD,OP⊥OC,
∵OD⊥PC,∴OD⊥平面OPC,
∴OD⊥OC,…(4分)
又∵OP⊥OC,∴OC⊥平面OPD,
∴OC⊥PD. …(6分)
解:(2)在矩形ABCD中,由(1)得OD⊥OC,∴AB=2AD,不妨设AD=1,则AB=2.
∵侧面PAB⊥底面ABCD,底面ABCD为矩形,
∴DA⊥平面PAB,CB⊥平面PAB,△DPA≌△DPA,
∴∠DPA为直线PD与平面PAB所成的角
∴∠DPA=30°,∠CPB=30°,$PA=PB=\sqrt{3}$,
∴DP=CP=2,∴△PDC为等边三角形,…(9分)
设PC的中点为M,连接DM,则DM⊥PC
在Rt△CBP中,过M作NM⊥PC,交PB于点N,则∠DMN为二面角D-PC-B的一个平面角.
由于∠CPB=30°,PM=1,∴在Rt△PMN中,$MN=\frac{{\sqrt{3}}}{3}$,$PN=\frac{{2\sqrt{3}}}{3}$,
∵$cos∠APB=\frac{3+3-4}{{2×\sqrt{3}×\sqrt{3}}}=\frac{1}{3}$,
∴$A{N^2}={(\frac{{2\sqrt{3}}}{3})^2}+3-2×\frac{{2\sqrt{3}}}{3}×\sqrt{3}×\frac{1}{3}=3$,
∴ND2=3+1=4,
∴$cos∠DMN=\frac{{{{(\frac{{\sqrt{3}}}{3})}^2}+3-4}}{{2×\frac{{\sqrt{3}}}{3}×\sqrt{3}}}=-\frac{1}{3}$,
即二面角D-PC-B的余弦值-$\frac{1}{3}$.…(12分)
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| A. | y=sin2x+cos2x | B. | y=sinx•cosx | C. | y=|cos2x| | D. | y=sin(2x+$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 3π+$\frac{9}{2}$ | B. | 3π+6 | C. | 5π+$\frac{9}{2}$ | D. | 5π+6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在等腰梯形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,∠ABC=60°,N是BC的中点,将ABCD绕AB旋转90°,得到梯形ABC′D′.
在等腰梯形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,∠ABC=60°,N是BC的中点,将ABCD绕AB旋转90°,得到梯形ABC′D′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com