
【题目】在公务员招聘中,既有笔试又有面试,某单位在2015年公务员考试中随机抽取100名考生的笔试成绩,按成绩分为5组[50,60),[60,70),[70,80),[80,90),[90,100],得到的频率分布直方图如图所示. 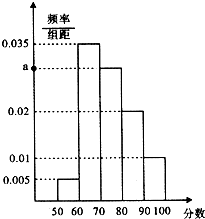
(1)求a值及这100名考生的平均成绩;
(2)若该单位决定在成绩较高的第三、四、五组中按分层抽样抽取6名考生进入第二轮面试,现从这6名考生中抽取3名考生接受单位领导面试,设第四组中恰有1名考生接受领导面试的概率.
【答案】
(1)解:由(0.005+0.035+a+0.02+0.01)×10=1,
得a=0.03.
平均成绩约为(55×0.005+65×0.035+75×0.03+85×0.02+95×0.01)×10=74.5
(2)解:第3,4,5组考生分别有30、20、10人,
按分层抽样,各组抽取人数为3,2,1
记第3组中3人为a1,a2,a3,第4组中2人为b1,b2,第5组中1人为c,
则抽取3人的所有情形为:
(a1,a2,a3),(a1,a2,b1),(a1,a2,b2),(a1,a2,c),(a1,a3,b1),
(a1,a3,b2),(a1,a3,c),(a1,a3,b1),(a2,a3,b2),(a2,a3,c),
(a1,b1,b2),(a1,b1,c),(a1,b2,c),(a2,b1,b2),(a2,b1,c),
(a2,b2,c),(a3,b1,b2),(a3,b1,c),(a3,b2,c),(b1,b2,c)共20种
第4组中恰有1人的情形有12种
∴ ![]()
【解析】(1)根据频率之和为1,即可求出a的值,再根据平均数的定义即可求出.(2)根据分层抽样,即可求出各组的人数,分别记第3组中3人为a1 , a2 , a3 , 第4组中2人为b1 , b2 , 第5组中1人为c,一一列举所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
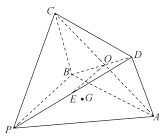
【题目】如图所示的几何体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为平面
为平面![]() 内任一点.
内任一点.
(1)在平面![]() 内,过
内,过![]() 点是否存在直线
点是否存在直线![]() 使
使![]() ?如果不存在,请说明理由,如果存在,请说明作法;
?如果不存在,请说明理由,如果存在,请说明作法;
(2)过![]() ,
, ![]() ,
, ![]() 三点的平面将几何体
三点的平面将几何体![]() 截去三棱锥
截去三棱锥![]() ,求剩余几何体
,求剩余几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,抛物线
,抛物线![]() ,
, ![]() 与
与![]() 有公共的焦点
有公共的焦点![]() ,
, ![]() 与
与![]() 在第一象限的公共点为
在第一象限的公共点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()
A. 仅有两个不同的离心率![]() 且
且![]() B. 仅有两个不同的离心率
B. 仅有两个不同的离心率![]() 且
且![]() C. 仅有一个离心率
C. 仅有一个离心率![]() 且
且![]() D. 仅有一个离心率
D. 仅有一个离心率![]() 且
且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一个平面去截正方体,对于截面的边界,有以下图形:①钝角三角形;②直角梯形;③菱形;④正五边形;⑤正六边形.则不可能的图形的选项为( )
A.③④⑤
B.①②⑤
C.①②④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在y=2x2上有一点P,它到A(1,3)的距离与它到焦点的距离之和最小,则点P的坐标是( )
A.(﹣2,1)
B.(1,2)
C.(2,1)
D.(﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量,有下列四个命题:
①若 ![]() .
.
② ![]() =(1,1),
=(1,1), ![]() =(2,x),若
=(2,x),若 ![]() 与
与 ![]() 平行,则x=2.
平行,则x=2.
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,则
|,则 ![]() 与
与 ![]() 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量 ![]() 同方向的单位向量为(
同方向的单位向量为( ![]() ).
).
其中真命题的序号为 . (写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com