由

,可得

.
点评:此题考查裂项相消法求数列前

项和,属基础题型.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本题满分10分)已知数列

满足

,
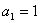
.
(Ⅰ) 求数列{

的前

项和

;
(Ⅱ)若存在

,使不等式

成立,求实数

的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列
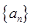
的前
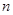
项和为
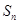
,且
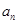
是
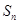
与2的等差中项,数列
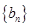
满足
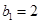
,点
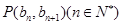
在直线
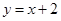
上,
(1)求数列
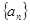
,
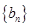
的通项公式;
(2)设
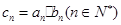
,求数列
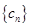
的前
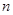
项和
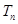
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知数列{
an}的前
n项和为
Sn,且
an是
Sn与2的等差中项,数列{
bn}中,
b1=1,点P(
bn,
bn+1)在直线
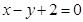
上。
(1)求
a1和
a2的值;
(2)求数列{
an},{
bn}的通项
an和
bn;
(3)设
cn=
an·
bn,求数列{
cn}的前n项和
Tn.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设数列
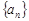
的前n项和S
n,且
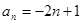
,则数列
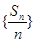
的前11项和为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)设
Sn是正项数列

的前
n项和,

.(I)求数列

的通项公式;(II)

的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若1+2+2
2+……+2
n-1 > 32 ,nÎN*,则n的最小值为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
本题14分) 已知数列
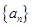
中,
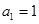
,
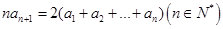
.
(1)求
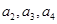
;
(2)求数列
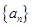
的通项
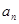
;
查看答案和解析>>

 阅读快车系列答案
阅读快车系列答案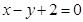 上。
上。