
 ,其中n∈N*.
,其中n∈N*.
 (s∈N*)的形式.
(s∈N*)的形式.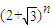 =
=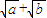 ,a、b∈N*,则
,a、b∈N*,则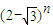 =
=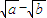 .再由 (
.再由 (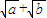 )(
)(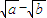 )=1,令 a=s,s∈N*,则必有 b=s-1,从而证得结论.
)=1,令 a=s,s∈N*,则必有 b=s-1,从而证得结论.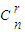 •2n-r•
•2n-r•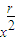 ,
, =3,解得r=6,展开式中含x3项的系数为
=3,解得r=6,展开式中含x3项的系数为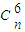 •2n-6=14,解得 n=7.
•2n-6=14,解得 n=7.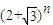 =
=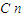 •2n•
•2n•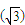 +
+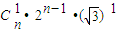 +
+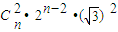
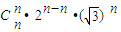 .
.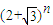 =x+
=x+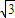 y=
y=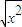 +
+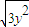 ,由于
,由于 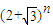 =
=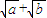 ,a、b∈N*,
,a、b∈N*,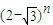 =
=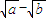 . …(7分)
. …(7分)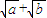 )(
)(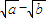 )=
)= •
•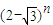 =1,
=1,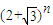 必可表示成
必可表示成 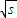
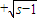 的形式,其中 s∈N*. …(10分)
的形式,其中 s∈N*. …(10分)

科目:高中数学 来源: 题型:
(08年山东卷理)(本小题满分12分)
已知函数![]() 其中n∈N*,a为常数.
其中n∈N*,a为常数.
(Ⅰ)当n=2时,求函数f(x)的极值;
(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年山东卷理)(本小题满分12分)
已知函数![]() 其中n∈N*,a为常数.
其中n∈N*,a为常数.
(Ⅰ)当n=2时,求函数f(x)的极值;
(Ⅱ)当a=1时,证明:对任意的正整数n,当x≥2时,有f(x)≤x-1.
查看答案和解析>>
科目:高中数学 来源: 题型:
(15分)已知函数![]() 其中n∈N*,a为常数.
其中n∈N*,a为常数.
(Ⅰ)当n =2时,求函数f(x)的极值;
(Ⅱ)当a =1时,证明:对任意的正整数n , 当x≥2时,有f(x)≤x-1.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都外国语学校高一(下)期中数学试卷(解析版) 题型:解答题
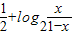 图象上任意两点,且
图象上任意两点,且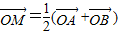 ,已知点M的横坐标为
,已知点M的横坐标为 .
.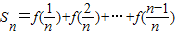 ,其中n∈N*且n≥2,
,其中n∈N*且n≥2,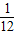 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn≤λ(Sn+1+1)对一切n∈N*都成立,试求λ的最小正整数值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com