Question

【题目】已知圆O的方程为x2+y2=1，直线l1过点A（3，0），且与圆O相切．
（1）求直线l1的方程；
（2）设圆O与x轴相交于P，Q两点，M是圆O上异于P，Q的任意一点，过点A且与x轴垂直的直线为l2 ， 直线PM交直线l2于点P′，直线QM交直线l2于点Q′．求证：以P′Q′为直径的圆C总经过定点，并求出定点坐标．

Answer 1

【答案】
（1）解：由题意，可设直线l1的方程为y=k（x﹣3），

即kx﹣y﹣3k=0

又点O（0，0）到直线l1的距离为 ，解得 ，

所以直线l1的方程为 ，

即 或

（2）解：对于圆O的方程x2+y2=1，令x=±1，即P（﹣1，0），Q（1，0）．

又直线l2方程为x=3，设M（s，t），则直线PM方程为 ．

解方程组 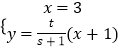，得 ，

同理可得： ．

所以圆C的圆心C的坐标为 ，半径长为 ，

又点M（s，t）在圆上，又s2+t2=1．故圆心C为 ，半径长 ．

所以圆C的方程为 ，

即 =0

即 ，

又s2+t2=1

故圆C的方程为 ，

令y=0，则（x﹣3）2=8，

所以圆C经过定点，y=0，则x= ，

所以圆C经过定点且定点坐标为

【解析】（1）由已知中直线l1过点A（3，0），我们可以设出直线的点斜式方程，化为一般式方程后，代入点到直线距离公式，根据直线与圆相切，圆心到直线的距离等于半径，可以求出k值，进而得到直线l1的方程；（2）由已知我们易求出P，Q两个点的坐标，设出M点的坐标，我们可以得到点P′与Q′的坐标（含参数），进而得到以P′Q′为直径的圆的方程，根据圆的方程即可判断结论．