
| A. | ①② | B. | ①②③ | C. | ③④ | D. | ①④ |
分析 由题意锐角三角形的性质,诱导公式、正弦定理逐一判断各个选项是否正确,从而得出结论.
解答 解:锐角三角形△ABC中,若A=2B,则B<$\frac{π}{4}$.
由2B+B+C=π,∴C=π-3B,∴sin3B=sinC正确,即①正确.
再根据$\frac{C}{2}$=$\frac{π}{2}$-$\frac{3B}{2}$,可得tan$\frac{C}{2}$=tan($\frac{π}{2}$-$\frac{3B}{2}$)=$\frac{1}{tan\frac{3B}{2}}$,∴tan$\frac{3B}{2}$•tan$\frac{C}{2}$=1,故②正确.
再根据C=π-3B<$\frac{π}{2}$,可得B>$\frac{π}{6}$,故③$\frac{π}{6}<B<\frac{π}{4}$正确.
由$\frac{a}{b}$=$\frac{sinA}{sinB}$=$\frac{sin2B}{sinB}$=2cosB,且$\frac{π}{6}$<B<$\frac{π}{4}$,可得cosB∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\frac{b}{a}$∈($\sqrt{2}$,$\sqrt{3}$),故④不对.
故选:B.
点评 本题主要考查锐角三角形的性质,诱导公式、正弦定理的应用,属于中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:选择题
下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为
③某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497--512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中命题正确的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
不等式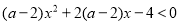 对一切
对一切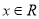 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.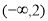 B.[-2,2] C.(-2,2] D.
B.[-2,2] C.(-2,2] D.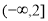
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都正确 | B. | 只有②正确 | C. | 只有①正确 | D. | 都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com