
【题目】如图,空间几何体![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 为
为![]() 中点.
中点.
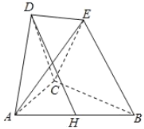
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 平面角的余弦值.
平面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,要证明
,要证明![]() 平面
平面![]() ,只需证明面
,只需证明面![]() ∥面
∥面![]() 即可.
即可.
(2)以点![]() 为原点,以
为原点,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
分别计算面![]() 的法向量
的法向量![]() ,面
,面![]() 的法向量可取
的法向量可取![]() ,并判断二面角为锐角,再利用
,并判断二面角为锐角,再利用![]() 计算即可.
计算即可.
(1)证明:分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
由平面![]() 平面
平面![]() ,且交于
,且交于![]() ,
,![]() 平面
平面![]() ,
,![]() 有
有![]() 平面
平面![]() ,
,
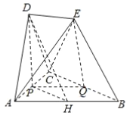
由平面![]() 平面
平面![]() ,且交于
,且交于![]() ,
,![]() 平面
平面![]() ,
,![]() 有
有![]() 平面
平面
![]() ,所以
,所以![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面
![]() ,由
,由![]() ,
,![]() 有,
有,![]() ∥
∥![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面
![]() ,所以
,所以![]() ∥平面
∥平面![]() ,
,
由![]() ∥平面
∥平面![]() ,
,![]() ∥平面
∥平面![]() ,
,![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() ,所以
,所以![]() ∥平面
∥平面![]()
(2)以点![]() 为原点,以
为原点,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系
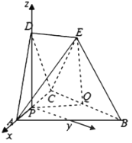
由![]() 面
面![]() ,所以面
,所以面![]() 的法向量可取
的法向量可取![]() ,
,
点![]() ,点
,点![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,
设面![]() 的法向量
的法向量![]() ,所以
,所以
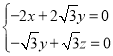 ,取
,取![]() ,
,
二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() 为锐角.
为锐角.
所以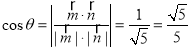


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点坐标为
的一个焦点坐标为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,过点
,过点![]() 的直线
的直线![]() (与
(与![]() 轴不重合)与椭圆
轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线C:
中,已知抛物线C:![]() (
(![]() )的焦点F在直线
)的焦点F在直线![]() 上,平行于x轴的两条直线
上,平行于x轴的两条直线![]() ,
,![]() 分别交抛物线C于A,B两点,交该抛物线的准线于D,E两点.
分别交抛物线C于A,B两点,交该抛物线的准线于D,E两点.
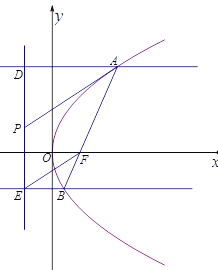
(1)求抛物线C的方程;
(2)若F在线段![]() 上,P是
上,P是![]() 的中点,证明:
的中点,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 过点Q(1,2),F为其焦点,过F且不垂直于x轴的直线l交抛物线E于A,B两点,动点P满足△PAB的垂心为原点O.
过点Q(1,2),F为其焦点,过F且不垂直于x轴的直线l交抛物线E于A,B两点,动点P满足△PAB的垂心为原点O.
(1)求抛物线E的方程;
(2)求证:动点P在定直线m上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,
中,![]() 是棱
是棱![]() 上动点,下列说法正确的是( ).
上动点,下列说法正确的是( ).
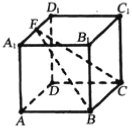
A.对任意动点![]() ,在平面
,在平面![]() 内存在与平面
内存在与平面![]() 平行的直线
平行的直线
B.对任意动点![]() ,在平面
,在平面![]() 内存在与平面
内存在与平面![]() 垂直的直线
垂直的直线
C.当点![]() 从
从![]() 运动到
运动到![]() 的过程中,
的过程中,![]() 与平面
与平面![]() 所成的角变大
所成的角变大
D.当点![]() 从
从![]() 运动到
运动到![]() 的过程中,点
的过程中,点![]() 到平面
到平面![]() 的距离逐渐变小
的距离逐渐变小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD,在点E,F处各放一个目标球,表演者先将母球放在点A处,通过击打母球,使其依次撞击点E,F处的目标球,最后停在点C处,若AE=50cm.EF=40cm.FC=30cm,∠AEF=∠CFE=60°,则该正方形的边长为( )
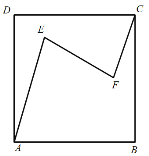
A.50![]() cmB.40
cmB.40![]() cmC.50cmD.20
cmC.50cmD.20![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com