
【题目】下列判断正确的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.命题“若![]() 则
则![]() ”的逆否命题为真
”的逆否命题为真
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.若命题p为真命题,命题q为假命题,则命题“![]() ”为真命题
”为真命题
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】定义区间![]() 的长度均为
的长度均为![]() ,其中
,其中![]()
(1)若函数![]() 的定义域为
的定义域为![]() 值域为
值域为![]() 写出区间长度
写出区间长度![]() 的最大值;
的最大值;
(2)若关于![]() 的不等式组
的不等式组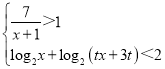 的解集构成的各区间长度和为6,求实数
的解集构成的各区间长度和为6,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 求证:关于
求证:关于![]() 的不等式
的不等式![]() 的解集构成的各区间的长度和为定值.
的解集构成的各区间的长度和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①命题“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题
中至少有一个不小于2”的逆命题是真命题
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题
”是一个真命题
③“![]() 的否定是“
的否定是“![]() ”
”
④已知![]() ,
,![]() 都是实数,“
都是实数,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区提供自行车出租,该景区有辆自行车供游客租赁使用,管理这些自行车的费用是每日![]() 元.根据经验,若每辆自行车的日租金不超过
元.根据经验,若每辆自行车的日租金不超过![]() 元,则自行车可以全部租出;若超出
元,则自行车可以全部租出;若超出![]() 元,则每超过
元,则每超过![]() 元,租不出的自行车就增加
元,租不出的自行车就增加![]() 辆.为了便于结算,每辆自行车的日租金
辆.为了便于结算,每辆自行车的日租金![]() (元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用![]() (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(1)求函数![]() 的解析式;
的解析式;
(2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月28日中国女排在世界杯第10轮比赛中,以![]() 的比分战胜塞尔维亚女排,从而在本次女排世界杯中取得10连胜,提前一轮卫冕世界杯冠军.世界杯是单循环赛制,中国女排要和11个对手轮番对决,比赛中以
的比分战胜塞尔维亚女排,从而在本次女排世界杯中取得10连胜,提前一轮卫冕世界杯冠军.世界杯是单循环赛制,中国女排要和11个对手轮番对决,比赛中以![]() 或
或![]() 取胜的球队积3分,负队积0分,而在比赛中以
取胜的球队积3分,负队积0分,而在比赛中以![]() 取胜的球队积2分,负队积1分,通过最终的总积分来决定最后的名次归属.下某网站上整理了2003年以来中国队与世界女排强队的50场比赛胜负情况如下表.
取胜的球队积2分,负队积1分,通过最终的总积分来决定最后的名次归属.下某网站上整理了2003年以来中国队与世界女排强队的50场比赛胜负情况如下表.
中国队和世界女排强队较量的胜负 | |||||||
年份 | 比赛类别 | 古巴 | 巴西 | 俄罗斯 | 意大利 | 美国 | 塞尔维亚 |
2003 | 世界杯 | ○ | ○ | ○ | ○ | ||
2004 | 奥运会(小组赛) | ● | ○ | ○ | |||
2004 | 奥运会(淘汰赛) | ○ | ○ | ||||
2006 | 世锦赛 | ● | ● | ○ | |||
2008 | 奥运会(小组赛) | ● | ● | ||||
2008 | 奥运会(淘汰赛) | ○ | ● | ○ | |||
2010 | 世锦赛 | ○ | ● | ● | |||
2011 | 世界杯 | ● | ● | ● | ○ | ||
2012 | 奥运会 | ● | ● | ○ | |||
2014 | 世锦赛 | ○ | ● | ○ | ● | ○ | |
2015 | 世界杯 | ○ | ○ | ● | |||
2016 | 奥运会(小组赛) | ○ | ○ | ● | ● | ||
2016 | 奥运会(淘汰赛) | ○ | |||||
2018 | 世锦赛(小组赛) | ○ | ● | ○ | |||
2018 | 世锦赛(复赛) | ○ | ● | ○ | |||
2019 | 世界杯 | ○ | ○ | ○ | ○ | ||
说明:○中国队获胜,●中国队败北,比分差:○表示分差为1(例如 | |||||||
(1)若根据表中数据进行推断:求中国队与巴西队比赛获得积分的平均数;
(2)现从中国队与美国比赛获胜的比赛视频中任意调取两场进行观看,求至少有一场是中国队以![]() 获胜的比赛的概率.
获胜的比赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com