
分析 (1)求出函数的导数,求出k的值,从而求出a的值,带入a的值,求出切线方程即可;
(2)问题转化为x≥-a-1对x∈(b-ea,2)恒成立,根据-a-1≤b-ea,即b≥ea-a-1对a∈[1,2]恒成立,设g(a)=ea-a-1,a∈[1,2],根据函数的单调性证明即可.
解答 解:(1)当k=0时,f(x)无极值,故k≠0.
由f'(x)=(kx+a+k)ex=0,
得$x=-\frac{a+k}{k}=-a-1$,
∴a+k=ak+k.
∵a≠0,∴k=1.
∵f'(0)=a+1=|2a-2|,∴a=3或$a=\frac{1}{3}$.
当a=3时,f(x)=(x+3)ex,f(0)=3,
∴l的方程为y=4x+3.
当$a=\frac{1}{3}$时,$f(x)=(x+\frac{1}{3}){e^x}$,$f(0)=\frac{1}{3}$,
∴l的方程为$y=\frac{4}{3}x+\frac{1}{3}$.
(2)证明:由题可知f'(x)=(x+a+1)ex≥0对x∈(b-ea,2)恒成立,
∵ex>0,∴x+a+1≥0,即x≥-a-1对x∈(b-ea,2)恒成立,
∴-a-1≤b-ea,即b≥ea-a-1对a∈[1,2]恒成立.
设g(a)=ea-a-1,a∈[1,2],则g'(a)=ea-1>0,
∴g(a)在[1,2]上递增,∴$g{(a)_{max}}=g(2)={e^2}-3$,∴b≥e2-3.
又(b-ea<2,∴e2-3≤b<ea+2.
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\left.\begin{array}{l}{α⊥γ}\\{β⊥γ}\end{array}\right\}$⇒α∥β | B. | $\left.\begin{array}{l}{m⊥l}\\{n⊥l}\end{array}\right\}$⇒m∥n | C. | $\left.\begin{array}{l}{m∥β}\\{l⊥m}\end{array}\right\}$⇒l∥β | D. | $\left.\begin{array}{l}{m∥n}\\{n⊥γ}\end{array}\right\}$⇒m⊥γ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
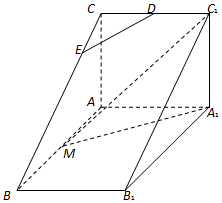 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
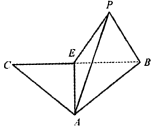 等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.
等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 80 | B. | 100 | C. | 120 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
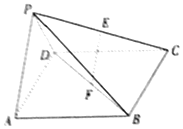 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分别为PC、BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com