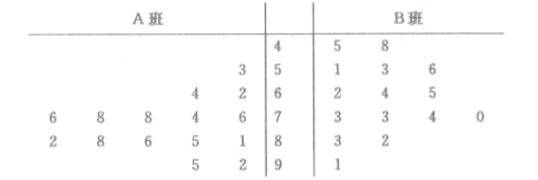
[题目]某学校.两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下.通过茎叶图比较两班数学兴趣小组成绩的平均值及方差①班数学兴趣小组的平均成绩高于班的平均成绩②班数学兴趣小组的平均成绩高于班的平均成绩③班数学兴趣小组成绩的标准差大于班成绩的标准差④班数学兴趣小组成绩的标准差大于班成绩的标准差其中正确结论的编号为( )A. ①③ B. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】某学校、两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下，通过茎叶图比较两班数学兴趣小组成绩的平均值及方差

①班数学兴趣小组的平均成绩高于班的平均成绩

②班数学兴趣小组的平均成绩高于班的平均成绩

③班数学兴趣小组成绩的标准差大于班成绩的标准差

④班数学兴趣小组成绩的标准差大于班成绩的标准差

其中正确结论的编号为（）

A. ①③ B. ①④ C. ②③ D. ②④

【答案】B

【解析】A班：53,63,64,76,74,78,78,76,81,85,86,88,82,92,95；

B班：45,48,51,53,56,62,64,65,73,73,74,70,83,82,91，

所以A班平均数为78，B班平均数为66，则A班平均成绩高于B班平均成绩；

由茎叶图可知，A班成绩相对集中，B班成绩相对分散，所以B班的标准差大于A班的标准差。

所以①④正确，故选B。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】直三棱柱中，，，，， .

（1）若，求直线与平面所成角的正弦值；

（2）若二面角的大小为，求实数的值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司生产一种化工产品，该产品若以每吨10万元的价格销售，每年可售出1000吨，若将该产品每吨分价格上涨，则每年的销售数量将减少，其中m为正常数，销售的总金额为y万元．

（1）当时，该产品每吨的价格上涨百分之几，可使销售总金额最大？

（2）当时，若能使销售总金额比涨价前增加，试设定m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某产品生产厂家根据以往销售经验得到下面有关生产销售的统计规律：每生产产品x（百台），其总成本为g（x）（万元），其中固定成本为2万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本），销售收入R（x）（万元）满足假设该产品产销平衡，试根据上述资料

（Ⅰ）要使工厂有盈利，产量x应控制在什么范围内；

（Ⅱ）工厂生产多少台产品时，可使盈利最多？

（Ⅲ）当盈利最多时，求每台产品的售价．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设关于x的方程2x2﹣ax﹣2=0的两根分别为α、β（α＜β），函数

（1）证明f（x）在区间（α，β）上是增函数；

（2）当a为何值时，f（x）在区间[α，β]上的最大值与最小值之差最小．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系中，已知椭圆：的离心率，左顶点为，过点作斜率为的直线交椭圆于点，交轴于点．

（1）求椭圆的方程；

（2）已知为的中点，是否存在定点，对于任意的都有，若存在，求出点的

坐标；若不存在说明理由；

（3）若过点作直线的平行线交椭圆于点，求的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某家具公司制作木质的椅子和书桌两种家具，需要木工和漆工两道工序，已知木工平均6个小时做一把椅子，10个小时做一张书桌，该公司每月木工最多有6000个工作时；漆工平均4个小时漆一把椅子，2个小时漆一张书桌，该公司每月漆工最多有2600个工作时又已知制作一把椅子和一张书桌的利润分别是15元和20元，根据以上条件，怎样安排每月的生产，才能获得最大的利润？