
【题目】为了治理空气污染,某市设![]() 个监测站用于监测空气质量指数
个监测站用于监测空气质量指数![]() ,其中在轻度污染区、中度污染区、重度污染区分别设有
,其中在轻度污染区、中度污染区、重度污染区分别设有![]() 、
、![]() 、
、![]() 个监测站,并以
个监测站,并以![]() 个监测站测得的
个监测站测得的![]() 的平均值为依据播报该市的空气质量.
的平均值为依据播报该市的空气质量.
(1)若某日播报的![]() 为
为![]() ,已知轻度污染区
,已知轻度污染区![]() 平均值为
平均值为![]() ,中度污染区
,中度污染区![]() 平均值为
平均值为![]() ,求重试污染区
,求重试污染区![]() 平均值;
平均值;
(2)如图是![]() 年
年![]() 月份
月份![]() 天的
天的![]() 的频率分布直方图,
的频率分布直方图,![]() 月份仅有
月份仅有![]() 天
天![]() 在
在![]() 内.
内.
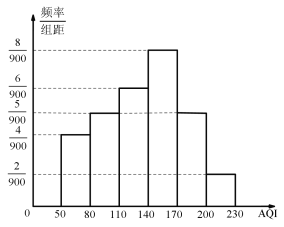
①某校参照官方公布的![]() ,如果周日
,如果周日![]() 小于
小于![]() 就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
就组织学生参加户外活动,以统计数据中的频率为概率,求该校学生周日能参加户外活动的概率;
②环卫部门从![]() 月份
月份![]() 不小于
不小于![]() 的数据中抽取两天的数据进行研究,求抽取的这两天中
的数据中抽取两天的数据进行研究,求抽取的这两天中![]() 值都在
值都在![]() 的概率.
的概率.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)设重度污染区![]() 平均值为
平均值为![]() ,根据题意可得出关于
,根据题意可得出关于![]() 的方程,进而可求得
的方程,进而可求得![]() 的值;
的值;
(2)①计算出![]() 月份
月份![]() 天中
天中![]() 不小于
不小于![]() 的天数,进而可求得该校学生周日能参加户外活动的概率;
的天数,进而可求得该校学生周日能参加户外活动的概率;
②由题意可知,![]() 在
在![]() 上的有
上的有![]() 天,编号分别设为
天,编号分别设为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 在
在![]() 上的有
上的有![]() 天,编号设为
天,编号设为![]() 、
、![]() ,列出所有的基本事件,并确定事件“抽取的这两天中
,列出所有的基本事件,并确定事件“抽取的这两天中![]() 值都在
值都在![]() ”所包含的基本事件,利用古典概型的概率公式可求得结果.
”所包含的基本事件,利用古典概型的概率公式可求得结果.
(1)设重度污染区![]() 平均值为
平均值为![]() ,则
,则![]() ,解得
,解得![]() ;
;
(2)①![]() 在
在![]() 上的有
上的有![]() 天,
天,
![]() 在
在![]() 上的有
上的有![]() 天,
天,
![]() 在
在![]() 上的有
上的有![]() 天,
天,
所以![]() 月份
月份![]() 不小于
不小于![]() 天的共
天的共![]() 天.
天.
即能参加户外活动的概率为![]() ;
;
②由①![]() 在
在![]() 上的有
上的有![]() 天,编号分别设为
天,编号分别设为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() 在
在![]() 上的有
上的有![]() 天,编号设为
天,编号设为![]() 、
、![]() ,
,
从![]() 天中抽取两天有:
天中抽取两天有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种.
种.
满足条件的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种,
种,
所以满足条件的概率为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】某植物学家培养出一种观赏性植物,会开出红花或黄花,已知该植物第一代开红花和黄花的概率都是![]() ,从第二代开始,若上一代开红花,则这一代开红花的概率是
,从第二代开始,若上一代开红花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() ;若上一代开黄花,则这一代开红花的概率是
;若上一代开黄花,则这一代开红花的概率是![]() ,开黄花的概率是
,开黄花的概率是![]() .记第n代开红花的概率为
.记第n代开红花的概率为![]() ,第n代开黄花的概率为
,第n代开黄花的概率为![]() .
.
(1)求![]() ;
;
(2)①证明:数列![]() 为等比数列;
为等比数列;
②第![]() 代开哪种颜色花的概率更大?
代开哪种颜色花的概率更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() :
:![]() 上的一点,其焦点为点
上的一点,其焦点为点![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线
处的切线![]() 交圆
交圆![]() :
:![]() 于不同的两点
于不同的两点![]() ,
,![]() .
.
(1)若点![]() ,求
,求![]() 的值;
的值;
(2)设点![]() 为弦
为弦![]() 的中点,焦点
的中点,焦点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省为迎接新高考,拟先对考生某选考学科的实际得分进行等级赋分,再按赋分后的分数从高分到低分划A、B、C、D、E五个等级,考生实际得分经赋分后的分数在到1之间.在等级赋分科学性论证时,对过去一年全省高考考生的该学科成绩重新赋分后进行分析,随机抽取2000名学生的该学科赋分后的成绩,得到如下频率分布直方图:(不考虑缺考考生的试卷)
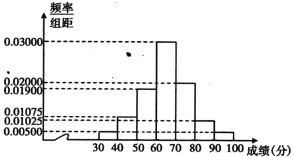
附:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<X<μ+3σ)=0.9974,![]() =14.59,∑(xi-
=14.59,∑(xi-![]() )2pi=213
)2pi=213
(1)求这2000名考生赋分后该学科的平均![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由频率分布直方图可以认为,学生经过赋分以后的成绩X服从正态分布X~N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2:
,σ2近似为样本方差s2:
(i)利用正态分布,求P(50.41<X<79.59);
(ii)某市有20000名高三学生,记Y表示这20000名高三学生中赋分后该学科等级为A等(即得分大于79.59)的学生数,利用(i)的结果,求EY.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标
.以坐标![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,建立极坐标系.
轴非负半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,
,![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,
,![]() .当
.当![]() 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学共有1000人,其中男生700人,女生300人,为了了解该校学生每周平均体育锻炼时间的情况以及经常进行体育锻炼的学生是否与性别有关(经常进行体育锻炼是指:周平均体育锻炼时间不少于4小时),现在用分层抽样的方法从中收集200位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如图.已知在样本数据中,有40位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理( )
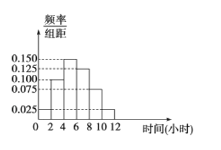
附: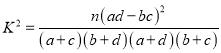 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A.有95%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
B.有90%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C.有90%的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D.有95%的把握认为“该校学生每周平均体育锻炼时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为原点,过原点的直线(不与
为原点,过原点的直线(不与![]() 轴垂直)与椭圆
轴垂直)与椭圆![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 、
、![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .问:
.问:![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
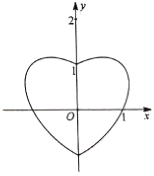
【题目】数学中有许多形状优美、寓意美好的曲线,如下图就是在平面直角坐标系的“心形曲线”,又名RC心形线.如果以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,其RC心形线的极坐标方程为
轴正半轴为极轴,建立极坐标系,其RC心形线的极坐标方程为![]() .
.
(1)求RC心形线的直角坐标方程;
(2)已知![]() 与直线
与直线![]() (
(![]() 为参数),若直线
为参数),若直线![]() 与RC心形线交于两点
与RC心形线交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com