

 (4a+4b)h'=a2+b2,得h'=
(4a+4b)h'=a2+b2,得h'=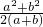 ,再在Rt△CDE中,利用勾股定理可得CE=
,再在Rt△CDE中,利用勾股定理可得CE= ,即得即棱台的高h的大小.
,即得即棱台的高h的大小.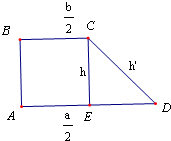
 (4a+4b)h'=a2+b2,得h'=
(4a+4b)h'=a2+b2,得h'=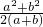
 (a-b)
(a-b)  =
=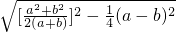 =
=




科目:高中数学 来源:高三数学教学与测试 题型:013
一个正四棱台上、下底面的边长分别为a,b,高为h,且侧面积等于两底面面积之和,则下列关系正确的是
[ ]




查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省太原五中高二(上)8月月考数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com