解:(1)求导数,得f'(x)=2x
3+3bx
2+2cx+d
∵函数f(x)在x=0和x=1处取得极值,
∴
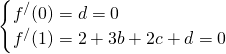
可得d=0,b=-

(c+1)
因此,f'(x)=2x
3-2(c+1)x
2+2cx=2x(x-1)(x-c)
∴当且仅当c≠0且c≠1时,函数在x=0和x=1处取得极值.
由此可得c的取值范围是{x|c≠0且c≠1}
(2)①∵函数f(x)在x=0处取得极大值
∴f(x)在x=0的左侧为增函数,在x=0的右侧为减函数,
因此,f'(x)在x=0的左侧大于0,在x=0的右侧小于于0,
又∵f'(x)=2x(x-1)(x-c),
∴f'(x)在(0,1)上为负数,得c<0且f'(x)在(c,0)上为正数
综上所述,得c的取值范围是(∞,0)
②因为c<0,得
当x<c或0<x<1时,f'(x)<0;当c<x<0或x>1时,f'(x)>0
∴函数f(x)在(-∞,c)和(0,1)上为减函数;在(c,0)和(1,+∞)上为增函数
因此,函数的极小值为f(c)和f(1),并且它们中的较小值就是函数f(x)的最小值
∵函数f(x)在x=1时取得最小值,
∴f(c)≥f(1),即

c
4-

(c+1)c
3+c
3+e≥

-

(c+1)+1+e
整理,得c
4-2c
3+2c-1≤0,即(c-1)
3(c+1)≤0
解这个不等式,得-1≤c≤1
∵c的取值范围是(∞,0),
∴c∈[-1,0),即为所求c的取值范围.
分析:(1)函数f(x)在极值点处的导数等于0,由此建立关于b、c、d的方程组并解之,可得d的值和b,c的关系式,再根据导数的三个零点互不相等,可得实数c的取值范围;
(2)①函数f(x)在x=0处取得极大值,说明f'(x)在x=0的左侧大于0,在x=0的右侧小于于0,从而得到x=c这个导数为零的点必须位于x=0的左侧,由此即可得到c的取值范围;
②根据导数的正负判断f(x)的单调性,可得函数的极小值为f(c)和f(1),且它们中的较小值就是函数f(x)的最小值,由此得f(c)≥f(1),建立关于c的不等式,整理得(c-1)
3(c+1)≤0,再结合c为负数,可得c的取值范围.
点评:本题给出多项式函数,在已知它的两个极值点的情况下求参数之间的关系式,并且讨论参数的取值范围,着重考查了利用导数研究函数的单调性和不等式的解法等知识,属于中档题.

 x4+bx3+cx2+dx+e(x∈R)在x=0和x=1处取得极值.
x4+bx3+cx2+dx+e(x∈R)在x=0和x=1处取得极值.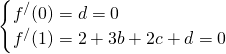 可得d=0,b=-
可得d=0,b=- (c+1)
(c+1) c4-
c4- (c+1)c3+c3+e≥
(c+1)c3+c3+e≥ -
- (c+1)+1+e
(c+1)+1+e

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<