
| A. | $(a+b)(\frac{1}{a}+\frac{1}{b})≥4$ | B. | a3+b3≥2ab2 | C. | $\sqrt{|a-b|}≥\sqrt{a}-\sqrt{b}$ | D. | a2+b2+2≥2a+2b |
分析 A.$(a+b)(\frac{1}{a}+\frac{1}{b})$=2+$\frac{b}{a}$+$\frac{a}{b}$,再利用基本不等式的性质即可得出;
B.作差:a3+b3-2ab2=(a-b)(a2+ab-b2),取a=1.5,b=2时,即可判断出正误;
C.分类讨论:当0≤a≤b时,左边≥0≥右边,此时成立;当0≤b<a时,平方作差$(\sqrt{|a-b|})^{2}-(\sqrt{a}-\sqrt{b})^{2}$═$2\sqrt{b}(\sqrt{a}-\sqrt{b})$,即可判断出正误.
D.作差配方可得:a2+b2+2-2a-2b=(a-1)2+(b-1)2≥0,即可判断出正误.
解答 解:对于A,∵a>0,b>0,∴$(a+b)(\frac{1}{a}+\frac{1}{b})$=2+$\frac{b}{a}$+$\frac{a}{b}$≥2+$2\sqrt{\frac{b}{a}•\frac{a}{b}}$=4,当且仅当a=b时取等号,因此恒成立.
对于B,a3+b3-2ab2=(a-b)(a2+ab-b2),取a=1.5,b=2时,a3+b3-2ab2<0,因此不恒成立;
对于C,当0≤a≤b时,左边≥0,右边≤0,此时成立;当0≤b<a时,$(\sqrt{|a-b|})^{2}-(\sqrt{a}-\sqrt{b})^{2}$=$(\sqrt{a}-\sqrt{b})$$(\sqrt{a}+\sqrt{b}-\sqrt{a}+\sqrt{b})$=$2\sqrt{b}(\sqrt{a}-\sqrt{b})$≥0,此时成立,
综上可得,不等式恒成立.
对于D,a2+b2+2-2a-2b=(a-1)2+(b-1)2≥0,∴a2+b2+2≥2a+2b,因此恒成立.
故选:B.
点评 本题考查了不等式与基本不等式的性质、“作差法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.
如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
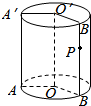 如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$.
如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2$\sqrt{2}$,$\frac{11}{3}$) | B. | (2$\sqrt{2}$,$\frac{11}{3}$] | C. | (2$\sqrt{3}$,4) | D. | (2$\sqrt{3}$,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com