练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，以坐标原点为极点，轴非负半轴为极轴建立极坐标系.已知曲线的极坐标方程为，直线的参数方程为（，为参数）

    （1）求曲线的直角坐标方程；

    （2）设直线与曲线交于、两点，点的直角坐标为，若，求直线的普通方程.

    【答案】（1）；（2）或

    【解析】

    （1）利用二倍角公式化简极坐标方程，再根据极坐标与直角坐标的对应关系得出曲线C的直角坐标方程；

    （2）将直线l的参数方程代入曲线的普通方程得出关于参数的一元二次方程，根据参数的几何意义得出两根，求出，，从而写出直线l的普通方程.

    （1）∵，

    ∴，∴，

    ∴曲线C的直角坐标方程为，即.

    （2）将直线l的参数方程代入曲线C的普通方程得：，

    ∴，，

    ∵，∴，

    解得，或，，

    ∴，∴，

    ∵，∴，

    ∴或．

    ∴直线的斜率，

    ∴直线的普通方程为或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一年之计在于春，一日之计在于晨，春天是播种的季节，是希望的开端.某种植户对一块地的个坑进行播种，每个坑播3粒种子，每粒种子发芽的概率均为，且每粒种子是否发芽相互独立.对每一个坑而言，如果至少有两粒种子发芽，则不需要进行补播种，否则要补播种.

    （1）当取何值时，有3个坑要补播种的概率最大？最大概率为多少？

    （2）当时，用表示要补播种的坑的个数，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，（常数且）.

    （Ⅰ）当与的图象相切时，求的值；

    （Ⅱ）设，若存在极值，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥P-ABC中，顶点P在底面ABC的投影G是ABC的外心，PB=BC＝2，则面PBC与底面ABC所成的二面角的大小为60，则三棱锥PABC的外接球的表面积为______

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点P在直线l:y=x-1上,若存在过点P的直线交抛物线于A,B两点,且|PA|=|AB|,则称点P为“正点”,那么下列结论中正确的是( )

    A.直线l上的所有点都是“正点”

    B.直线l上仅有有限个点是“正点”

    C.直线l上的所有点都不是“正点”

    D.直线l上有无穷多个点(但不是所有的点)是“正点”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）令，若在区间上不单调，求的取值范围；

    （2）当时，函数的图象与轴交于两点，，且，又是的导函数.若正常数，满足条件，.试比较与0的关系，并给出理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中）.

    （1）讨论函数的极值；

    （2）对任意，成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区某农产品近几年的产量统计如下表:

    （1）根据表中数据，建立关于的线性回归方程；

    （2）若近几年该农产品每千克的价格 (单位:元）与年产量满足的函数关系式为，且每年该农产品都能售完.

    ①根据（1）中所建立的回归方程预测该地区年该农产品的产量；

    ②当为何值时，销售额最大？

    附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为： ， .

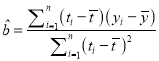    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，椭圆：经过点，且点为其一个焦点.

    （1）求椭圆的方程；

    （2）设椭圆与轴的两个交点为，，不在轴上的动点在直线上运动，直线，分别与椭圆交于点，，证明：直线通过一个定点，且的周长为定值.

    查看答案和解析>>

    同步练习册答案