
ЁОЬтФПЁПЬьЫЎЪаЕквЛДЮСЊПМКѓЃЌФГаЃЖдМзЁЂввСНИіЮФПЦАрЕФЪ§бЇПМЪдГЩМЈНјааЗжЮіЃЌ
ЙцЖЈЃКДѓгкЛђЕШгк120ЗжЮЊгХауЃЌ120ЗжвдЯТЮЊЗЧгХауЃЎЭГМЦГЩМЈКѓЃЌ
ЕУЕНШчЯТЕФ![]() СаСЊБэЃЌЧввбжЊдкМзЁЂввСНИіЮФПЦАрШЋВП110ШЫжаЫцЛњГщШЁ1ШЫЮЊгХауЕФИХТЪЮЊ
СаСЊБэЃЌЧввбжЊдкМзЁЂввСНИіЮФПЦАрШЋВП110ШЫжаЫцЛњГщШЁ1ШЫЮЊгХауЕФИХТЪЮЊ![]() .
.
гХау | ЗЧгХау | КЯМЦ | |
МзАр | 10 | ||
ввАр | 30 | ||
КЯМЦ | 110 |
ЃЈ1ЃЉЧыЭъГЩЩЯУцЕФСаСЊБэЃЛ
ЃЈ2ЃЉИљОнСаСЊБэЕФЪ§ОнЃЌШєАД99.9%ЕФПЩППадвЊЧѓЃЌФмЗёШЯЮЊЁАГЩМЈгыАрМЖгаЙиЯЕЁБЃЛ
ЃЈ3ЃЉШєАДЯТУцЕФЗНЗЈДгМзАргХауЕФбЇЩњжаГщШЁвЛШЫЃКАбМзАргХауЕФ10УћбЇЩњДг2ЕН11НјааБрКХЃЌЯШКѓСНДЮХзжРвЛУЖОљдШЕФїЛзгЃЌГіЯжЕФЕуЪ§жЎКЭЮЊБЛГщШЁШЫЕФађКХЁЃЪдЧѓГщЕН9КХЛђ10КХЕФИХТЪЁЃ
ВЮПМЙЋЪНгыСйНчжЕБэЃК![]() ЁЃ
ЁЃ
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
ЁОД№АИЁПЃЈ1ЃЉ
гХау | ЗЧгХау | КЯМЦ | |
МзАр | 10 | 50 | 60 |
ввАр | 20 | 30 | 50 |
КЯМЦ | 30 | 80 | 110 |
ЃЈ2ЃЉМЦЫуЕУЕНK2= Ёж7.487ЃМ10.828ЃЎвђДЫАД99.9%ЕФПЩППадвЊЧѓЃЌВЛФмШЯЮЊЁАГЩМЈгыАрМЖгаЙиЯЕЁБ
ЃЈ3ЃЉГщЕН9КХЛђ10КХЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃК
ЫМТЗЗжЮіЃКДЫРрЮЪЬтЃЈ1ЃЉЃЈ2ЃЉжБНгЬзгУЙЋЪНЃЌОЙ§МЦЫуЁАПЈЗНЁБЃЌгыЪ§БэЖдБШЃЌзїГіНсТлЁЃЃЈ3ЃЉЪЧЕфаЭЕФЙХЕфИХаЭИХТЪЕФМЦЫуЮЪЬтЃЌШЗЖЈСНИіЁАЪТМўЁБЪ§ЃЌШЗЖЈЦфБШжЕЁЃ
НтЃКЃЈ1ЃЉ 4Зж
гХау | ЗЧгХау | КЯМЦ | |
МзАр | 10 | 50 | 60 |
ввАр | 20 | 30 | 50 |
КЯМЦ | 30 | 80 | 110 |
ЃЈ2ЃЉИљОнСаСЊБэжаЕФЪ§ОнЃЌЕУЕНK2= Ёж7.487ЃМ10.828ЃЎвђДЫАД99.9%ЕФ
ПЩППадвЊЧѓЃЌВЛФмШЯЮЊЁАГЩМЈгыАрМЖгаЙиЯЕЁБ 8Зж
ЃЈ3ЃЉЩшЁАГщЕН9Лђ10КХЁБЮЊЪТМўAЃЌЯШКѓСНДЮХзжРвЛУЖОљдШЕФїЛзгЃЌГіЯжЕФЕуЪ§ЮЊЃЈxЃЌyЃЉЃЎЫљгаЕФЛљБОЪТМўгаЃКЃЈ1ЃЌ1ЃЉЁЂЃЈ1ЃЌ2ЃЉЁЂЃЈ1ЃЌ3ЃЉЁЂЁЁЂЃЈ6ЃЌ6ЃЉЙВ36ИіЃЎЪТМўAАќКЌЕФЛљБОЪТМўгаЃКЃЈ3ЃЌ6ЃЉЁЂЃЈ4ЃЌ5ЃЉЁЂЃЈ5ЃЌ4ЃЉЁЂЃЈ6ЃЌ3ЃЉЁЂЃЈ5ЃЌ5ЃЉЁЂЃЈ4ЃЌ6ЃЉЃЈ6ЃЌ4ЃЉЙВ7ИіЃЎЫљвдP(A)= ![]() ЃЌМДГщЕН9КХЛђ10КХЕФИХТЪЮЊ
ЃЌМДГщЕН9КХЛђ10КХЕФИХТЪЮЊ![]() ЃЎ 12Зж
ЃЎ 12Зж


 УћаЃУћЪІХргХзївЕБОМгКЫаФЪдОэЯЕСаД№АИ
УћаЃУћЪІХргХзївЕБОМгКЫаФЪдОэЯЕСаД№АИ ШЋГЬН№ОэЯЕСаД№АИ
ШЋГЬН№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏЮЊЭЦГівЛПю6ДчДѓЦСЪжЛњЃЌЯжЖд500УћИУЪжЛњЪЙгУепЃЈ200УћХЎадЃЌ300УћФаадЃЉНјааЕїВщЃЌЖдЪжЛњНјааДђЗжЃЌДђЗжЕФЦЕЪ§ЗжВМБэШчЯТЃК
ХЎадгУЛЇЃК
ЗжжЕЧјМф |
|
|
|
|
|
ЦЕЪ§ | 20 | 40 | 80 | 50 | 10 |
ФаадгУЛЇЃК
ЗжжЕЧјМф |
|
|
|
|
|
ЦЕЪ§ | 45 | 75 | 90 | 60 | 30 |
ЃЈ1ЃЉШчЙћЦРЗжВЛЕЭгк70ЗжЃЌОЭБэЪОИУгУЛЇЖдЪжЛњЁАШЯПЩЁБЃЌЗёдђОЭБэЪОЁАВЛШЯПЩЁБЃЌЭъГЩЯТСа![]() СаСЊБэЃЌВЂЛиД№ЪЧЗёга
СаСЊБэЃЌВЂЛиД№ЪЧЗёга![]() ЕФАбЮеШЯЮЊадБ№ЖдЪжЛњЕФЁАШЯПЩЁБгаЙиЃК
ЕФАбЮеШЯЮЊадБ№ЖдЪжЛњЕФЁАШЯПЩЁБгаЙиЃК
ХЎадгУЛЇ | ФаадгУЛЇ | КЯМЦ | |
ЁАШЯПЩЁБЪжЛњ | |||
ЁАВЛШЯПЩЁБЪжЛњ | |||
КЯМЦ |
ИНЃК
| 0.05 | 0.01 |
| 3.841 | 6.635 |
![]()
ЃЈ2ЃЉИљОнЦРЗжЕФВЛЭЌЃЌдЫгУЗжВуГщбљДгФаадгУЛЇжаГщШЁ20УћгУЛЇЃЌдкет20УћгУЛЇжаЃЌДгЦРЗжВЛЕЭгк80ЗжЕФгУЛЇжаШЮвтГщШЁ2УћгУЛЇЃЌЧѓ2УћгУЛЇжаЦРЗжаЁгк90ЗжЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯђСП![]() ЃЌ
ЃЌ ![]() ЃЎЩш
ЃЎЩш![]() (tЮЊЪЕЪ§)ЃЎ
(tЮЊЪЕЪ§)ЃЎ
ЃЈЂёЃЉШє![]() ЃЌЧѓЕБ
ЃЌЧѓЕБ![]() ШЁзюаЁжЕЪБЪЕЪ§tЕФжЕЃЛ
ШЁзюаЁжЕЪБЪЕЪ§tЕФжЕЃЛ
ЃЈЂђЃЉШє![]() ЁЭ
ЁЭ![]() ЃЌЮЪЃКЪЧЗёДцдкЪЕЪ§tЃЌЪЙЕУЯђСП
ЃЌЮЪЃКЪЧЗёДцдкЪЕЪ§tЃЌЪЙЕУЯђСП![]() Ѓ
Ѓ![]() КЭЯђСП
КЭЯђСП![]() ЕФМаНЧЮЊ
ЕФМаНЧЮЊ![]() ЃЌШєДцдкЃЌЧыЧѓГіtЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЌШєДцдкЃЌЧыЧѓГіtЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌНЧ
жаЃЌНЧ![]() ЫљЖдЕФБпЗжБ№ЮЊ
ЫљЖдЕФБпЗжБ№ЮЊ![]() ЃЌЧв
ЃЌЧв![]() .
.
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() гы
гы![]() ЕФЭМЯѓгаШ§ИіВЛЭЌЕФНЛЕуЃЌЧѓЪЕЪ§
ЕФЭМЯѓгаШ§ИіВЛЭЌЕФНЛЕуЃЌЧѓЪЕЪ§![]() ЕФЗЖЮЇЃЛ
ЕФЗЖЮЇЃЛ
ЃЈ2ЃЉЬжТл![]() ЕФЕЅЕїад.
ЕФЕЅЕїад.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-5ЃКВЛЕШЪНбЁНВ
вбжЊКЏЪ§fЃЈxЃЉ=|2xЃЋ1|+|2xЃa|ЃЎ
ЃЈIЃЉШєfЃЈxЃЉЕФзюаЁжЕЮЊ2ЃЌЧѓaЕФжЕЃЛ
ЃЈIIЃЉШєfЃЈxЃЉЁм|2xЃ4|ЕФНтМЏАќКЌ[Ѓ2ЃЌЃ1]ЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈЦфжа
ЃЈЦфжа![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЌ
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉШє![]() НігавЛИіМЋжЕЕуЃЌЧѓ
НігавЛИіМЋжЕЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉжЄУїЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гаСНИіСуЕу
гаСНИіСуЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШЋМЏU=RЃЌA={x|x2Љ2xЉ3Ём0}ЃЌB={x|2ЁмxЃМ5}ЃЌC={x|xЃОa}ЃЎ
ЃЈ1ЃЉЧѓAЁЩЃЈUBЃЉЃЛ
ЃЈ2ЃЉШєAЁШC=CЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЮЊСтаЮЃЌЫФБпаЮ
ЮЊСтаЮЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЌЩш
ЮЊЦНааЫФБпаЮЃЌЩш![]() гы
гы![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
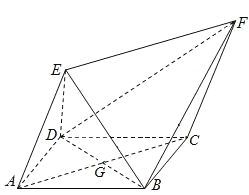
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓШ§РтзЖ
ЃЌЧѓШ§РтзЖ![]() ЕФЬхЛ§ЃЎ
ЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com