
【题目】如图,四边形![]() 的两条对角线
的两条对角线![]() 相交于
相交于![]() ,现用五种颜色(其中一种为红色)对图中四个三角形
,现用五种颜色(其中一种为红色)对图中四个三角形![]() 进行染色,且每个三角形用一种颜色图染.
进行染色,且每个三角形用一种颜色图染.
(1)若必须使用红色,求四个三角形![]() 中有且只有一组相邻三角形同色的染色方法的种数;
中有且只有一组相邻三角形同色的染色方法的种数;
(2)若不使用红色,求四个三角形![]() 中所有相邻三角形都不同色的染色方法的种数.
中所有相邻三角形都不同色的染色方法的种数.

【答案】(1)144(2)![]() 种
种
【解析】试题分析:(1)分两种情况: ![]() 同时染红色,
同时染红色, ![]() 同时染的不是红色,然后根据分类计数加法原理可得结果;(2)分三种情况:一共使用了四种颜色,使用了三种颜色,使用了两种颜色,然后根据分类计数加法原理可得结果.
同时染的不是红色,然后根据分类计数加法原理可得结果;(2)分三种情况:一共使用了四种颜色,使用了三种颜色,使用了两种颜色,然后根据分类计数加法原理可得结果.
试题题解析:(1)同色的相邻三角形共有![]() 种,不妨假设为
种,不妨假设为![]() ,
,
①若![]() 同时染红色,则另外两个三角形共有
同时染红色,则另外两个三角形共有![]() 种染色方法,因此这种情况共有
种染色方法,因此这种情况共有![]() 种染色方法;
种染色方法;
②若![]() 同时染的不是红色,则它们的染色有
同时染的不是红色,则它们的染色有![]() 种,另外两个三角形一个必须染红色,所以这两个三角形共有
种,另外两个三角形一个必须染红色,所以这两个三角形共有![]() ,因此这种情况共有
,因此这种情况共有![]() 种染色方法.
种染色方法.
综上可知有且只有一组相邻三角形同色的染色方法的种数为![]() 种;
种;
(2)因为不用红色,则只有四种颜色.
若一共使用了四种颜色,则共有![]() 种染色方法;若只使用了三种颜色,则必有一种颜色使用了两次,且染在对顶的区域,所以一共有
种染色方法;若只使用了三种颜色,则必有一种颜色使用了两次,且染在对顶的区域,所以一共有![]() 种染色方法;若只使用了两种颜色,则两种颜色都使用了两次,且各自染在一组对顶区域,所以共有
种染色方法;若只使用了两种颜色,则两种颜色都使用了两次,且各自染在一组对顶区域,所以共有![]() 种染色方法.综上可知所有相邻三角形都不同色的染色方法的种数为
种染色方法.综上可知所有相邻三角形都不同色的染色方法的种数为![]() 种.
种.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润![]() (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费![]() 和年利润
和年利润![]() (
(![]() )进行了统计,列出了下表:
)进行了统计,列出了下表:
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合![]() 与
与![]() 的关系,请你帮助建立
的关系,请你帮助建立![]() 关于
关于![]() 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)
(2)小李决定选择对数回归模型拟合![]() 与
与![]() 的关系,得到了回归方程:
的关系,得到了回归方程: ![]() ,并提供了相关指数
,并提供了相关指数![]() .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据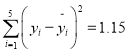 )
)
参考公式:相关指数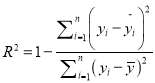
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 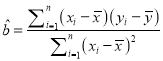 ,
, ![]() .参考数据:
.参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品每件进价9元,售价20元,每天可卖出69件.若售价降低,销售量可以增加,且售价降低![]() 元时,每天多卖出的件数与
元时,每天多卖出的件数与![]() 成正比.已知商品售价降低3元时,一天可多卖出36件.
成正比.已知商品售价降低3元时,一天可多卖出36件.
(Ⅰ)试将该商品一天的销售利润表示成![]() 的函数;(Ⅱ)该商品售价为多少元时一天的销售利润最大?
的函数;(Ⅱ)该商品售价为多少元时一天的销售利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
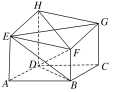
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=
=1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=![]() (a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线![]() 和直线
和直线![]() 交于点
交于点![]() .以
.以![]() 为起点,再从曲线
为起点,再从曲线![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为![]() .若
.若![]() 去九寨沟;若
去九寨沟;若![]() 去泰山;若
去泰山;若![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.
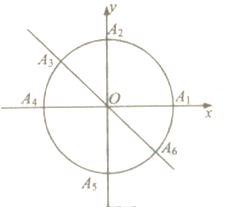
(1)若从![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线![]() 上取点
上取点![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点![]() 在曲线
在曲线![]() 上运动,若点
上运动,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax+ln(x+1)(a∈R).
(1)当a=2时,求函数f(x)的极值点;
(2)若函数f(x)在区间(0,1)上恒有f′(x)>x,求实数a的取值范围;
(3)已知a<1,c1>0,且cn+1=f′(cn)(n=1,2,…),证明数列{cn}是单调递增数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com