
【题目】已知![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设等差数列![]() 的公差为
的公差为![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比数列.可得
成等比数列.可得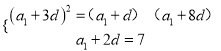 ,解之得即可得出数列
,解之得即可得出数列![]() 的通项公式;
的通项公式;
2)由(1)得![]() ,则
,则![]() ,由裂项相消法可求数列
,由裂项相消法可求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)设数列![]() 的公差为
的公差为![]() ,且
,且![]() 由题意得
由题意得![]() ,
,
即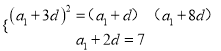 ,解得
,解得![]() ,
,
所以数列![]() 的通项公式
的通项公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【题型】解答题
【结束】
18
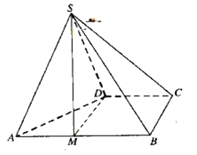
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】通过随机询问100名性别不同的大学生是否爱好踢毽子,得到如下的列联表:

随机变量![]() 经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
经计算,统计量K2的观测值k0≈4.762,参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”
C. 有97.5%以上的把握认为“爱好该项运动与性别有关”
D. 有97.5%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项的和记为Sn.如果a4=-12,a8=-4.
(1)求数列{an}的通项公式;
(2)求Sn的最小值及其相应的n的值;
(3)从数列{an}中依次取出a1,a2,a4,a8,…,![]() ,…,构成一个新的数列{bn},求{bn}的前n项和
,…,构成一个新的数列{bn},求{bn}的前n项和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)经过点(1,
=1(a>b>0)经过点(1,![]() ),且焦距为2
),且焦距为2![]() .
.
(1)求椭圆C方程;
(2)椭圆C的左,右焦点分别为F1,F2,过点F2的直线l与椭圆C交于A,B两点,求△F2AB面积S的最大值并求出相应直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.在党和政府强有力的抗疫领导下,我国控制住疫情后,一方面防止境外疫情输入,另一方面逐步复工复产,减轻经济下降对企业和民众带来的损失.为降低疫情影响,某厂家拟在2020年举行某产品的促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按
为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按![]() 元来计算)
元来计算)
(1)将2020年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,函数
,函数![]() .
.
(1)求![]() 的最小正周期及
的最小正周期及![]() 图象的对称轴方程;
图象的对称轴方程;
(2)若先将![]() 的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移
的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 内的所有零点之和.
内的所有零点之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com