Question

16．如图是一个算法流程图，则输出的n值为10．

Answer 1

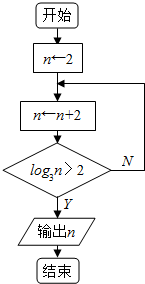
分析 先要通读程序框图，看到程序中有循环结构，然后代入初值，看是否进入循环体，是就执行循环体，写清每次循环的结果；不是就退出循环，看清要输出的是何值．

解答 解：执行循环体前，n=2，
第一次执行循环体后，n=4，log₃4＜2，不满足退出循环的条件，
第二次执行循环体后，n=6，log₃6＜2，不满足退出循环的条件，
第三次执行循环体后，n=8，log₃8＜2，不满足退出循环的条件，
第四次执行循环体后，n=10，log₃10＞2，满足退出循环的条件，
故输出的n为：10．
故答案为：10

点评 本题考查程序框图．要掌握常见的当型、直到型循环结构；以及会判断条件结构，并得到条件结构的结果；在已知框图的条件下，可以得到框图的结果．