

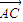 为平面EFD的法向量,求出平面CEF的法向量,利用向量的夹角公式,即可求二面角C-EF-D的大小;
为平面EFD的法向量,求出平面CEF的法向量,利用向量的夹角公式,即可求二面角C-EF-D的大小;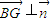 ,则可得G为CD的中点时,BG∥平面CEF.
,则可得G为CD的中点时,BG∥平面CEF. (I)证明:建立如图所示的坐标系,则A(2,0,0),B(2,2,0),C(0,2,0),F(2,2,1),E(0,0,2)
(I)证明:建立如图所示的坐标系,则A(2,0,0),B(2,2,0),C(0,2,0),F(2,2,1),E(0,0,2)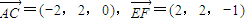
 =-2×2+2×2+(-1)×0=0
=-2×2+2×2+(-1)×0=0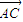 为平面EFD的法向量
为平面EFD的法向量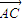 =(-2,2,0)
=(-2,2,0) =(x,y,1),∴
=(x,y,1),∴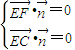
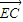 =(0,2,-2),
=(0,2,-2),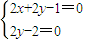
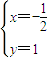
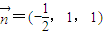
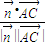 =
=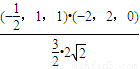 =
=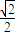
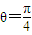
 ,又
,又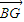 =(-2,y,0)
=(-2,y,0) =(-2,y-2,0)•(-
=(-2,y-2,0)•(- ,1,1)=1+y-2+0=0
,1,1)=1+y-2+0=0

科目:高中数学 来源: 题型:
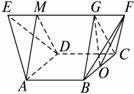
 (2013•泰安一模)如图在多面体ABCDEF中,ABCD为正方形,ED⊥平面ABCD,FB∥ED,且AD=DE=2BF=2.
(2013•泰安一模)如图在多面体ABCDEF中,ABCD为正方形,ED⊥平面ABCD,FB∥ED,且AD=DE=2BF=2.查看答案和解析>>
科目:高中数学 来源: 题型:
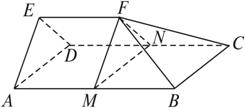
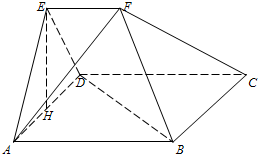 如图,在多面体ABCD-EF中,四边形ABCD为正方形,EF∥AB,EF⊥EA,AB=2EF,∠AED=90°,AE=ED,H为AD的中点.
如图,在多面体ABCD-EF中,四边形ABCD为正方形,EF∥AB,EF⊥EA,AB=2EF,∠AED=90°,AE=ED,H为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.5 C.6 D.
B.5 C.6 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com