
【题目】已知![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 是
是![]() 展开式中所有无理项的二项式系数和,数列
展开式中所有无理项的二项式系数和,数列![]() 是各项都大于1的数组成的数列,试用数学归纳法证明:
是各项都大于1的数组成的数列,试用数学归纳法证明:![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=x﹣aex(a∈R),x∈R,已知函数y=f(x)有两个零点x1 , x2 , 且x1<x2 .
(1)求a的取值范围;
(2)证明: ![]() 随着a的减小而增大;
随着a的减小而增大;
(3)证明x1+x2随着a的减小而增大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中混装着9个大小相同的球(编号不同),其中5只白球,4只红球,为了把红球与白球区分开来,采取逐只抽取检查,若恰好经过5次抽取检查,正好把所有白球和红球区分出来了,则这样的抽取方式共有__________种(用数字作答) .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]()
![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥A﹣BCD及其侧视图、俯视图如图所示,设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP. 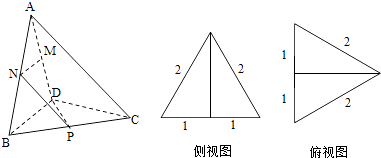
(1)证明:P是线段BC的中点;
(2)求二面角A﹣NP﹣M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次![]() 函数,分别从集合
函数,分别从集合![]() 和
和![]() 中随机取一个数
中随机取一个数![]() 和
和![]() 得到数对
得到数对![]() .
.
(1)若![]() ,
, ![]() ,求函数
,求函数![]() 有零点的概率;
有零点的概率;
(2)若![]() ,
, ![]() ,求函数
,求函数![]() 在区间
在区间![]() 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法总数.
(1)全体排成一行,其中男生必须排在一起;
(2)全体排成一行,男、女各不相邻;
(3)全体排成一行,其中甲不在最左边,乙不在最右边;
(4)全体排成一行,其中甲、乙、丙三人从左至右的顺序不变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是两个不共线的非零向量.
是两个不共线的非零向量.
(1)设![]() ,
,![]() ,
,![]() ,那么当实数t为何值时,A,B,C三点共线;
,那么当实数t为何值时,A,B,C三点共线;
(2)若![]() ,
,![]() 且
且![]() 与
与![]() 的夹角为60°,那么实数x为何值时
的夹角为60°,那么实数x为何值时![]() 的值最小?最小值为多少?
的值最小?最小值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com