
����Ŀ��ij�����̴����ˮ����ֳ������һ��С��Ϻ���������ȡ40ֻ����ͳ�ƣ�����������ͳ�ƽ����ͼ�� 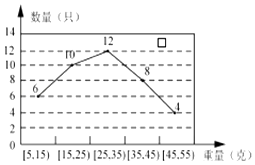
��1�����¼�AΪ����������С��Ϻ����ȡһֻ������������35g��С��Ϻ������P��A���Ĺ���ֵ��
��2������������С��Ϻ100ǧ�ˣ��Թ�������С��Ϻ��������
��3��Ϊ��Ӧ�г������˽�����С��Ϻ�ĿڸУ��þ����̽���40ֻС��Ϻ�ֳ������ȼ������±���
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
������g�� | [5��25�� | [25��45�� | [45��55] |
���ֲ������ȡ10ֻ���������ȡ3ֻƷ������XΪ�鵽����Ʒ����������鵽����Ʒ��������
���𰸡�
��1���⣺����40ֻС��Ϻ������������35g��С��Ϻ��6+10+12=28��ֻ��
���� ![]() ��
��
��2���⣺��ͳ��ͼ�п��Թ���ÿֻС��Ϻ������ ![]()
= ![]() ���ˣ�
���ˣ�
���Թ���100ǧ�ˣ�С��Ϻ������Լ��100000��28.5��3509��ֻ��
��3���⣺������֪��ȡһ��Ʒ������Ʒ������Ʒ�ֱ�Ϊ4ֻ��5ֻ��1ֻ��X=0��1��2��3
��ɵ� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]()
���� ![]() ��
��
����������1������40ֻС��Ϻ������������35g��С��Ϻ��6+10+12��ֻ�������ùŵ���ʼ��㹫ʽ���ɵó�����2�������ƽ�������ɵô�ͳ��ͼ�п��Թ���ÿֻС��Ϻ����������3��������֪��ȡһ��Ʒ������Ʒ������Ʒ�ֱ�Ϊ4ֻ��5ֻ��1ֻ��X=0��1��2��3�����ó����ηֲ��еĸ��� �ļ��㹫ʽ���ɵó���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ����ѧ·��Ҫ����A��B��C�������к��̵Ƶ�·�ڣ���֪����A��B��C����·��������Ƶĸ��������� ![]() ��
�� ![]() ��
�� ![]() ���������ʱͣ����ʱ��������40�롢20�롢80�룬���ڸ�·���Ƿ����������������ģ�
���������ʱͣ����ʱ��������40�롢20�롢80�룬���ڸ�·���Ƿ����������������ģ�
��1��������ͬѧ����ѧ·���ڵ�����·���״�������Ƶĸ��ʣ���
��2��������ͬѧ����ѧ·�����������ͣ������ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=a��x+lnx����a��0����g��x��=x2 ��
��1����f��x����ͼ����x=1��������ǡ��Ҳ��g��x��ͼ������ߣ���ʵ��a��ֵ��
��2����������[1��2]�ϵ�������������ȵ�ʵ��x1 �� x2��x1��x2 �� ����f��x2����f��x1����g��x2����g��x1������������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����2an+1=an+an+2+k��n��N* �� k��R������a1=2��a3+a5=��4��
��1����k=0��������{an}��ǰn���Sn��
��2����a4=��1��������{an}��ͨ�ʽan ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʵ��x��y�����Լ������ 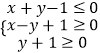 ����һ������Ͷ�����εõ��ĵ����ֱ�Ϊa��b������z=2ax+by�ڵ㣨2����1����ȡ�����ֵ�ĸ���Ϊ�� ��
����һ������Ͷ�����εõ��ĵ����ֱ�Ϊa��b������z=2ax+by�ڵ㣨2����1����ȡ�����ֵ�ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��������x2=4y�ϵĶ��㣬��P��x���ϵ���Ӱ��Q����A��8��7������|PA|+|PQ|����СֵΪ�� ��
A.7
B.8
C.9
D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲE�� ![]() ��������Ϊ
��������Ϊ ![]() ��F1 �� F2�ֱ����������ҽ��㣬�Ҵ���ֱ��l��ʹF1 �� F2����l�ĶԳƵ�ǡ��ΪԲC��x2+y2��4mx��2my+5m2��4=0��m��R��m��0����һ��ֱ���������˵㣮
��F1 �� F2�ֱ����������ҽ��㣬�Ҵ���ֱ��l��ʹF1 �� F2����l�ĶԳƵ�ǡ��ΪԲC��x2+y2��4mx��2my+5m2��4=0��m��R��m��0����һ��ֱ���������˵㣮
��1������ԲE�ķ��̣�
��2����ֱ��l��������y2=2px��p��0���ཻ��A��B���㣬����F1A��F1B����ԲE�ֱ��ཻ�ڵ�M��N����̽�����Ƿ��������D�����ҽ���p��Dʱ���ܴ���m��ʹ��F1�����߶�MNΪֱ����Բ�ڣ������ڣ��������D���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ƕ�����R�ϵ��溯������f��x����ͼ�����ֱ��x=1�Գƣ�
��1����֤��f��x��������Ϊ4�����ں�����
��2����f��x��= ![]() ��0��x��1������x��[��5����4]ʱ������f��x���Ľ���ʽ��
��0��x��1������x��[��5����4]ʱ������f��x���Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�Ķ���C��ƽ����ڣ���ֱ��BC��ƽ������ɽ�Ϊ15�㣬����B��ƽ����ϵ���ӰΪ��O��������A���O�ľ������ʱ��ֱ��CD��ƽ������ɽǵ�����ֵΪ �� 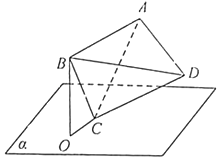
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com