
【题目】如图所示的几何体,是将高为2、底面半径为1的圆柱沿过旋转轴的平面切开后,将其中一半沿切面向右水平平移后形成的封闭体.![]() 分别为
分别为![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点,
的中点,![]() 为弧
为弧![]() 的中点.
的中点.
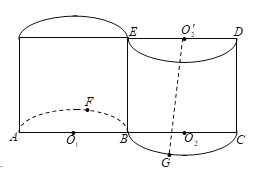
(1)求直线![]() 与底面
与底面![]() 所成的角的大小;
所成的角的大小;
(2)求异面直线![]() 与
与![]() 所成的角的大小(结果用反三角函数值表示).
所成的角的大小(结果用反三角函数值表示).
科目:高中数学 来源: 题型:
【题目】如图所示,在五棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 是边长为2的正三角形,四边形
是边长为2的正三角形,四边形![]() 为正方形,
为正方形,![]() ,且
,且![]() ,
,![]() 是
是![]() 的重心,
的重心,![]() 是正方形
是正方形![]() 的中心.
的中心.
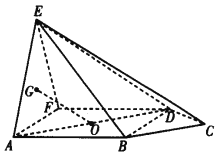
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在![]() 到
到![]() 之间,将测量结果按如下方式分成六组:第1组
之间,将测量结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组得到的频率分布直方图,以频率近似概率.
,如图是按上述分组得到的频率分布直方图,以频率近似概率.
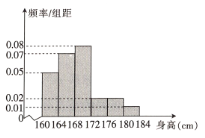
(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)试估计该校高一年级全体男生身高的平均数(同一组中的数据用该组区间的中点值代表)与中位数;
(3)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年“双十一”全网销售额达![]() 亿元,相当于全国人均消费
亿元,相当于全国人均消费![]() 元,同比增长
元,同比增长![]() ,监测参与“双十一”狂欢大促销的
,监测参与“双十一”狂欢大促销的![]() 家电商平台有天猫、京东、苏宁易购、网易考拉在内的综合性平台,有拼多多等社交电商平台,有敦煌网、速卖通等出口电商平台.某大学学生社团在本校
家电商平台有天猫、京东、苏宁易购、网易考拉在内的综合性平台,有拼多多等社交电商平台,有敦煌网、速卖通等出口电商平台.某大学学生社团在本校![]() 名大一学生中采用男女分层抽样,分别随机调查了若干个男生和
名大一学生中采用男女分层抽样,分别随机调查了若干个男生和![]() 个女生的网购消费情况,制作出男生的频率分布表、直方图(部分)和女生的茎叶图如下:
个女生的网购消费情况,制作出男生的频率分布表、直方图(部分)和女生的茎叶图如下:

男生直方图
分组(百元) | 男生人数 | 频率 |
|
|
|
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|
|
|
合计 |
|

女生茎叶图
(1)请完成频率分布表的三个空格,并估计该校男生网购金额的中位数(单位:元,精确到个位).
(2)若网购为全国人均消费的三倍以上称为“剁手党”,估计该校大一学生中的“剁手党”人数为多少?从抽样数据中网购不足![]() 元的同学中随机抽取
元的同学中随机抽取![]() 人发放纪念品,则
人发放纪念品,则![]() 人都是女生的概率为多少?
人都是女生的概率为多少?
(3)用频率估计概率,从全市所有高校大一学生中随机调查![]() 人,求其中“剁手党”人数的分布列和期望.
人,求其中“剁手党”人数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区不同身高![]() 的未成年男性的体重平均值
的未成年男性的体重平均值![]() 如下表:
如下表:
身高x(cm) | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
体重y(kg) | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 |
已知![]() 与
与![]() 之间存在很强的线性相关性,
之间存在很强的线性相关性,
(Ⅰ)据此建立![]() 与
与![]() 之间的回归方程;
之间的回归方程;
(Ⅱ)若体重超过相同身高男性体重平均值的![]() 倍为偏胖,低于
倍为偏胖,低于![]() 倍为偏瘦,那么这个地区一名身高
倍为偏瘦,那么这个地区一名身高![]() 体重为
体重为![]()
![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?
参考数据:![]()
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,且
,且![]() ,
,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为等边三角形,
为等边三角形,![]() 是棱
是棱![]() 上的一点,设
上的一点,设![]() (
(![]() 与
与![]() 不重合).
不重合).
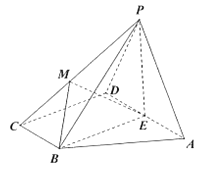
(1)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,求二面角
时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两铁路线垂直相交于站![]() ,若已知
,若已知![]() 千米,甲火车从
千米,甲火车从![]() 站出发,沿
站出发,沿![]() 方向以
方向以![]() 千米
千米![]() 小时的速度行驶,同时乙火车从
小时的速度行驶,同时乙火车从![]() 站出发,沿
站出发,沿![]() 方向,以
方向,以![]() 千米
千米![]() 小时的速度行驶,至
小时的速度行驶,至![]() 站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
(1)求甲、乙两车的最近距离(用含![]() 的式子表示);
的式子表示);
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为![]() 小时,问
小时,问![]() 为何值时
为何值时![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com