
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 的单调性;
的单调性;
(2)当![]() 且
且![]() 时,
时,![]() ,求函数
,求函数![]() 在
在![]() 上的最小值;
上的最小值;
(3)当![]() 时,
时,![]() 有两个零点
有两个零点![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() 在
在![]() 上单调递增(2)
上单调递增(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)求得函数的导数![]() ,结合导数的符号,即可求得函数的单调性;
,结合导数的符号,即可求得函数的单调性;
(2)由![]() ,求得
,求得![]() ,分类讨论求得函数的单调性与极值,进而求得函数的最小值,得到答案.
,分类讨论求得函数的单调性与极值,进而求得函数的最小值,得到答案.
(3)由![]() ,根据题意,得到
,根据题意,得到![]() ,
,![]() ,
,
两式相减,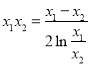 ,令
,令![]() ,得到函数
,得到函数![]() ,利用导数求得函数的单调性与最值,即可求解.
,利用导数求得函数的单调性与最值,即可求解.
(1)由题意,函数![]() ,则
,则![]() ,
,
又∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递增.
上单调递增.
(2)由![]() ,则
,则![]() ,
,
(1)当![]() 时,
时,![]() ,
,![]() ,
,
此时图数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
∴函数![]() 在
在![]() 处取得最小值,即
处取得最小值,即![]() ;
;
(2)当![]() 时,令
时,令![]() ,
,
当![]() 时,即当
时,即当![]() ,
,![]() ,
,![]() ,
,
此时函数![]() 在区间
在区间![]() 上单调递减,函数
上单调递减,函数![]() 在
在![]() 处取得最小值,
处取得最小值,
即![]() ;
;
综上所得![]() .
.
(3)证明:根据题意,![]() ,
,
∵![]() ,
,![]() 是函数
是函数![]() 的两个零点,
的两个零点,
∴![]() ,
,![]() .
.
两式相减,可得![]() ,即
,即![]() ,
,
∴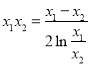 ,则
,则 ,
, .
.
令![]() ,
,![]() ,则
,则 .
.
记![]() ,
,![]() ,则
,则![]() .
.
又∵![]() ,∴
,∴![]() 恒成立,故
恒成立,故![]() ,即
,即![]() .
.
可得 ,∴
,∴![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两台机床同时加工直径为10cm的零件,为了检验零件的质量,从零件中各随机抽取6件测量,测得数据如下(单位:mm):
甲:99,100,98,100,100,103;
乙:99,100,102,99,100,100.
(1)分别计算上述两组数据的平均数和方差
(2)根据(1)的计算结果,说明哪一台机床加工的零件更符合要求.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从含有两件正品a1,a2和一件次品b1的3件产品中每次任取1件,
每次取出后不放回,连续取两次.
(1)求取出的两件产品中恰有一件次品的概率;
(2)如果将“每次取出后不放回”这一条件换成“每次取出后放回”,则取出的两件产品中恰有一件次品的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,记
,记![]() 为与原点距离等于
为与原点距离等于![]() 的全体直线所成的集合.问:是否存在常数
的全体直线所成的集合.问:是否存在常数![]() ,使得对任意的直线
,使得对任意的直线![]() ,均存在
,均存在![]() 、
、![]() ,
,![]() 、
、![]() 分别过
分别过![]() 与椭圆
与椭圆![]() 的交点
的交点![]() 、
、![]() ,且有
,且有![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知菱形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() ,如图2所示.
,如图2所示.

(Ⅰ)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的椭圆C经过点M(2,1),N(![]() ,-
,-![]() ).
).
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海的国家会展中心举办.国家展、企业展、经贸论坛、高新产品汇集……首届进博会高点纷呈.一个更加开放和自信的中国,正用实际行动为世界构筑共同发展平台,展现推动全球贸易与合作的中国方案.
某跨国公司带来了高端智能家居产品参展,供购商洽谈采购,并决定大量投放中国市场.已知该产品年固定研发成本30万美元,每生产一台需另投入90美元.设该公司一年内生产该产品![]() 万台且全部售完,每万台的销售收入为
万台且全部售完,每万台的销售收入为![]() 万美元,
万美元,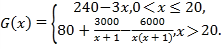
(1)写出年利润![]() (万美元)关于年产量
(万美元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com